Содержание
MM152
Конкурсная задача ММ152 (6 баллов)
Сколькими способами можно разрезать квадрат на 10 квадратов. Два разрезания считаются неразличимыми, если в итоге получится поровну квадратов каждого размера.
Решение
Приведу решение Олега Полубасова.
Для любого разбиения прямоугольника на k квадратов можно выписать систему из k-1 однородных линейных уравнений, связывающих размеры квадратов, поэтому размеры квадратов относятся как рациональные числа.
План таков: найти все решения уравнения 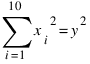 (1) в натуральных числах, где xi взаимно просты в совокупности. Затем отбросить наборы, из которых не удаётся сложить квадрат.
Перебор кажется необозримым, но Г. Дьюдени в задаче «Стёганое одеяло миссис Перкинс» предположил (а в 1964 г. Дж. Конуэй в статье с одноимённым названием доказал), что для 10 квадратов y не может превышать 9.
С другой стороны, ясно, что y ≥ 4, поэтому количество перебираемых вариантов оказывается совсем небольшим.
Дополнительным отсечением служит тот очевидный факт, что сумма размеров двух наибольших квадратов не должна превышать размера разбиваемого квадрата, то есть xi + xj ≤ y.
Удобнее оперировать переменными zi = (xi2 - 1), w = y2 - 10, тогда уравнение перепишется как
(1) в натуральных числах, где xi взаимно просты в совокупности. Затем отбросить наборы, из которых не удаётся сложить квадрат.
Перебор кажется необозримым, но Г. Дьюдени в задаче «Стёганое одеяло миссис Перкинс» предположил (а в 1964 г. Дж. Конуэй в статье с одноимённым названием доказал), что для 10 квадратов y не может превышать 9.
С другой стороны, ясно, что y ≥ 4, поэтому количество перебираемых вариантов оказывается совсем небольшим.
Дополнительным отсечением служит тот очевидный факт, что сумма размеров двух наибольших квадратов не должна превышать размера разбиваемого квадрата, то есть xi + xj ≤ y.
Удобнее оперировать переменными zi = (xi2 - 1), w = y2 - 10, тогда уравнение перепишется как 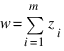 (2), где m ≤ 10, zi ∈ { 3, 8, 15, 24, 35, 48, 63}, w ∈ {6, 15, 26, 39, 54, 71}.
(2), где m ≤ 10, zi ∈ { 3, 8, 15, 24, 35, 48, 63}, w ∈ {6, 15, 26, 39, 54, 71}.
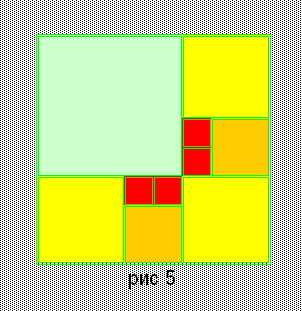
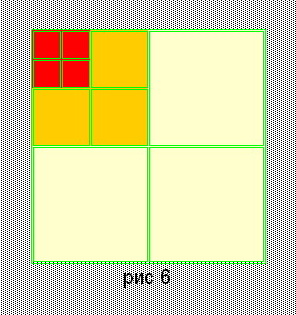
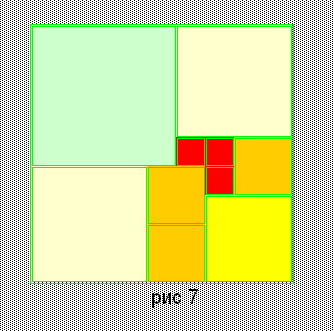
Решения последнего уравнения сведены в таблицу. Вторая колонка - решения уравнения (2); третья колонка - взаимно простые решения уравнения (1), удовлетворяющие условию xi + xj ≤ y; четвертая - номера рисунков, для решений, из которых можно сложить квадрат.
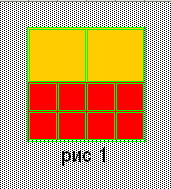
| 1. | 6=2* 3 | 2*22+8*12 = 42 | Рис. 1 |
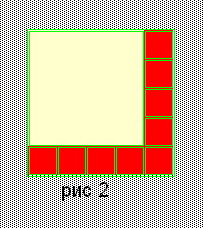
| 2. | 15=15 | 1*42+9*12 = 52 | Рис. 2 |
| 3. | 15=5* 3 | 5*22+5*12 = 52 | |
| 4. | 26=15+8+3 | ||
| 5. | 26=8+6* 3 | 1*32+6*22+3*12 = 62 | |
| 6. | 39=24+15 | ||
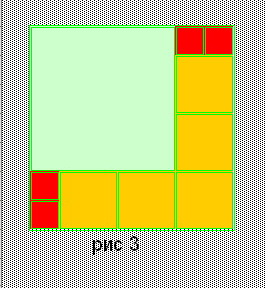
| 7. | 39=24+5* 3 | 1*52+5*22+4*12 = 72 | Рис. 3 |
| 8. | 39=2*15+3* 3 | ||
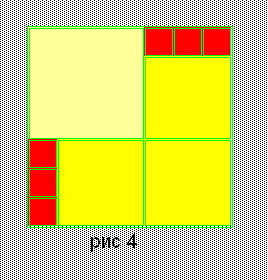
| 9. | 39=15+3* 8 | 1*42+3*32+6*12 = 72 | Рис. 4 |
| 10. | 39=15+8* 3 | 1*42+8*22+1*12 = 72 | |
| 11. | 39=3*8+5*3 | 3*32+5*22+2*12 = 72 | |
| 12. | 54=48+2*3 | ||
| 13. | 54=35+2*8+3 | ||
| 14. | 54=2*24+2*3 | ||
| 15. | 54=24+2*15 | ||
| 16. | 54=24+3*8+2*3 | 1*52+3*22+2*22+4*12 = 82 | Рис. 5 |
| 17. | 54=3*15+3*3 | 3*42+3*22+4*12 = 82 | Рис. 6 |
| 18. | 54=2*15+3*8 | 2*42+3*32+5*12 = 82 | |
| 19. | 54=2*15+8*3 | ||
| 20. | 54=6*8+2*3 | 6*32+2*22+2*12 = 82 | |
| 21. | 71=63+8 | ||
| 22. | 71=48+15+8 | ||
| 23. | 71=48+8+5*3 | ||
| 24. | 71=35+24+4*3 | ||
| 25. | 71=2*24+15+8 | ||
| 26. | 71=2*24+8+5*3 | ||
| 27. | 71=24+2*15+8+3*3 | 1*52+2*42+1*32+3*22+3*12 = 92 | Рис. 7 |
| 28. | 71=24+15+4*8 | 1*52+1*42+4*32+4*12 = 92 | |
| 29. | 71=24+4*8+5*3 | 1*52+4*32+5*22 = 92 | |
| 30. | 71=4*15+8+3 | 4*42+1*32+1*22+4*12 = 92 | |
| 31. | 71=3*15+8+6*3 | 3*42+1*32+6*22 = 92 | |
| 32. | 71=2*15+4*8+3*3 | 2*42+4*32+3*22+1*12 = 92 | |
| 33. | 71=15+7*8 | 1*42+7*32+2*12 = 92 |
Ответ: 7 способов.
Обсуждение
Назначая цену задачу, я планировал давать 6 призовых баллов тем участникам, которые решат задачу так же, как сделал это я. То есть найдут все 7 разбиений, но не получат строгого доказательства полноты решения. За наличие доказательства или нахождение других разбиений (в эту альтернативу я не верил, но чем черт не шутит?) планировались дополнительные баллы. На чем базировалась моя уверенность в отсутствии других разбиений? Так же как и многие участники, я перебирал разбиения квадрата nxn на квадраты со взаимно простыми в совокупности длинами сторон. Осуществляя полный перебор на последовательных n, я пришел к твердому убеждению (но не доказательству, что при больших n (я добрался до 15) минимальное число квадратов заведомо больше 10.
На Wolfram'е (http://mathworld.wolfram.com/MrsPerkinssQuilt.html) для небольших приведены минимальные количества квадратов в разбиении квадрата nxn. Сначала эта зависимость вполне монотонна. Однако не все так просто. Квадрат 40×40 нельзя порезать менее чем на 16 квадратов со взаимно простыми сторонами. А квадрат 41×41 можно разрезать на 15 квадратов. Вот таблица, сопоставляющая числу квадратов в разрезании те n, для которых это число минимально.
| s(n) | n |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 6 | 3 |
| 7 | 4 |
| 8 | 5 |
| 9 | 6,7 |
| 10 | 8,9 |
| 11 | 11-13 |
| 12 | 14-17 |
| 13 | 18-23 |
| 14 | 24-29 |
| 15 | 30-39,41 |
| 16 | 40,42-53 |
| 17 | 54-70 |
| 18 | 71-91 |
| 19 | 92-120,122,126 |
| 20 | 121,123-125,127-154,157,158 |
Сергей Половинкин составил список, в котором представлены разрезания квадрата на k квадратов, для всех k, не превышающих 12.
| k | f(k) |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 1 |
| 7 | 1 |
| 8 | 2 |
| 9 | 4 |
| 10 | 7 |
| 11 | 16 |
| 12 | 30 |
Интересно, что начиная с k = 7 идет почти точное удвоение числа разбиений на каждом шаге. Между прочим, данная последовательность отсутствует в OEIS. Полагаю, следует восполнить этот пробел. Готовя эту задачу прошлым летом, я оптимистично начинал со случая k = 13. Добравшись до разбиений квадрата 17×17 и получив несколько десятков разбиений квадрата на 13 квадратов, я понял, что погорячился и переключился на случай k=11 . Его я просчитал до конца (если чего-то не прозевал). Но, к сожалению, не могу найти летнюю тетрадку, чтобы свериться с результатами Сергея.
Наиболее знаменитой задачей, связанной с разрезанием квадрата, является задача о разрезании квадрата на попарно различные квадраты. В свое время Н.Н.Лузин полагал, что этого сделать нельзя. Однако вскоре было найдено решение. Основная идея - сопоставить каждому разрезанию прямоугольника на квадраты некую схему электрической цепи. Подробнее об этом можно почитать, например, в «Кванте» №5 за 2010 год (там этот вопрос рассматривается сразу в двух статьях). Разумеется, напрашивается свести к рассмотрению электрических цепей и нашу задачу. Сам я, изучая такой подход пришел к выводу, что «хрен редьки не слаще». Однако Олег Полубасов и Анатолий Казмерчук оказались более настойчивы преуспели в возникающем переборе уже не квадратов, но цепей.
Награды
За правильное решение задачи ММ152 и обоснование его полноты Олег Полубасов и Анатолий Казмерчук получают по 9 призовых баллов. За правильное решение и любопытные (хотя не абсолютно строгие) соображения по обоснованию полноты решения Николай Дерюгин получает 7 призовых баллов. Столько же баллов получает Сергей Половинкин за верное решение и рассмотрение случаев разрезания на другое число квадратов. За верное решение Виктор Филимоненков получает 6 призовых баллов. Алексей Волошин получает 4 призовых балла. Александр Князев и Елизавета Евдокимова - по 2 призовых балла, Екатерина Шарпанова - 1 призовой балл.
Эстетическая оценка - 4.8 балла
Разбор задачи ММ152 подготовил Владимир Лецко
Примечание:
Согласно OEIS (http://oeis.org/A232484), f(11) = 18, а f(12) = 40 (т. е. списки Сергея Половинкина для этих значений не полны)
См. также https://arxiv.org/pdf/1308.5420.pdf