Содержание
ММ38
Конкурсная задача ММ8 (3 балла)
Обозначим через f(n) количество последовательностей длины n из нулей, единиц и двоек таких, что никакие две единицы и никакие две двойки не могут стоять в них подряд. Найти явную формулу для f(n).
Решение
Обозначим 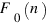 количество таких последовательностей, оканчивающихся на 0,
количество таких последовательностей, оканчивающихся на 0, 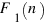 - оканчивающихся на 1,
- оканчивающихся на 1, 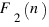 - оканчивающихся на 2.
- оканчивающихся на 2.
Тогда 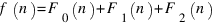 .
.
Так как к любой последовательности можно приписать 0, не нарушив условий задачи, то
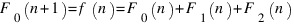 .
.
Так как 1 можно приписать только к последовательности, оканчивающейся на 0 или 2, то 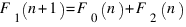 .
.
Аналогично 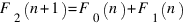 .
.
Складывая, получаем:
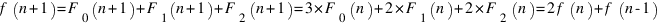 .
.
Очевидно, что f(1) = 3 и f(2) = 7.
Таким образом, имеем следующую рекуррентное уравнение: f(n+1) = 2f(n) + f(n-1) при n > 2, f(1) = 3, f(2) = 7.
Характеристическое уравнение для полученного линейного рекуррентного соотношения второго порядка имеет вид 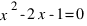 .
.
Корни характеристического уравнения: 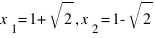 ,
а общее решение -
,
а общее решение - 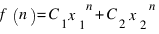 .
.
Учитывая начальные условия, находим:
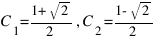 .
.
Окончательно имеем: 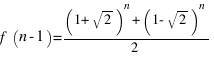 .
.
Обсуждение
Последовательность, описная в обсуждаемой задаче, состоит из числителей наилучших рациональных приближений числа 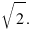
С рядом других ситуаций, в которых возникает f(n), можно познакомиться в онлайн-энциклопедии математических последовательностей. Наша f(n) представлена там под номером A001333.
Награды
За правильное решение этой задачи Влад Франк, Мигель Митрофанов и Иван Козначеев получают по 3 призовых балла.