

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ100
Юбилейная задача представляет собой по сути целый букет задач, связанных общей тематикой и общими идеями. Часть подзадач - известные (но, с учетом их красоты, на мой взгляд, недостаточно известные) утверждения. Другие - новые (хотелось бы надеяться не только для меня).
Конкурсная задача ММ100 (17 баллов)
Пусть Sn множество всех перестановок множества Mn = {1,2,3…,n}
1. Найти и обосновать рекуррентное выражение количества перестановок g из
Sn таких, что для всех k из Mn g(k) может отличаться от k:
a) не более, чем на 1;
b) не более, чем на 2.
2. Рассмотрим произвольный элемент из Sn и произвольное a из Mn. Найти вероятность того, что a входит в цикл длины k.
3. Для произвольного элемента g из Sn найти:
a) математическое ожидание количества циклов длины k;
b) математическое ожидание количества циклов;
c) моду циклового вида (учитываются количество и длина циклов);
d) полагая k > n/5, найти вероятность того, что в g будет хотя бы один цикл
длины k.
4. Вспомним, что Sn является группой относительно композиции перестановок.
Обозначим s(n,k) = | {gk | g ∈ Sn} |, q(n,k) = s(n,k)/n!:
a) найти 20 наименьших значений s(n,k);
b) возможно ли равенство q(n,k) = 1/2 для нечетных k.
ММ99
Результат пpедлагаемой задачи учитывается дважды:
В Большом Маpафоне и в конкуpсе задач на поиск закономерности.
Конкурсная задача ММ99 (З-5) (8 баллов)
Продолжить последовательность 0,0,1,0,3,4,6,0,1,8,6,4,6,6,13,8…
Подсказка: при продолжении данная последовательность через некоторое время поведет себя весьма регулярно, а затем и вовсе стабилизируется.
ММ98
Предлагаемая задача не входит в тематический конкурс. Результат учитывается только в основном Маpафоне.
Конкурсная задача ММ98 (7 баллов)
Васю Пупкина заслали в тыл врага с целью выявить секретный код, ввод которого
предотвратит термоядерный взрыв.
Вася незамеченным проник в святая святых и сфотографировал секретный код
на мобильник. Но, пробираясь к своим, Вася потерял мобильник и теперь пытается
вспомнить код.
- Помню только, что код состоял из трех чисел, расположенных строго в порядке
возрастания - удрученно докладывает Вася руководству.
- А какие числа: двузначные, трехзначные,..?
- Не помню…
- Вася, но ведь ты по образованию математик! Вспомни, может быть, среди
чисел были какие-нибудь особенные: квадраты, кубы,..
- Нет, таких не было, но я припоминаю, что сложив сумму квадратов цифр
одного из этих чисел с суммой кубов цифр другого я получил сумму этих
двух чисел.
- Это уже кое-что! Но код можно вводить только один раз. В случае неверного
кода взрыв неминуем. Вспоминай дальше.
- Вспомнил! Эти числа могли служить количествами вершин, граней и,
соответственно, ребер некоторого выпуклого многогранника. Я даже мысленно
представил себе подходящий многогранник.
- Хорошо. Дальше.
- Так… Каждое из чисел представлялось в виде суммы двух натуральных
квадратов.
- Что еще? Ах, да! По крайней мере два из них были простыми…
- А еще У двух чисел были одинаковые значения функции Эйлера…
- Все! Больше ничего не помню.
1. Помогите Васе спасти человечество.
2. Какие из пришедших на память Васе соотношений избыточны?
ММ97
Результат пpедлагаемой задачи учитывается дважды:
В Большом Маpафоне и в конкуpсе задач на поиск закономерности.
Конкурсная задача ММ97 (З-4) (3 балла)
Продолжить последовательность 10, 21, 55, 253, 1081,…
ММ96
Предлагаемая задача не входит в тематический конкурс. Результат учитывается только в основном Маpафоне.
Конкурсная задача ММ96 (6 баллов)
Двое играют в такую игру:
С помощью идеального генератора случайных чисел выбирают натуральное число
из интервала 1..10100. Если выпавшее число свободно от квадратов, первый
игрок платит второму 200 рублей, в противном случае второй игрок платит
первому 300 рублей. И т.д.
Кому выгодна такая игра?
ММ95
Результат пpедлагаемой задачи учитывается дважды:
В Большом Маpафоне и в конкуpсе задач на поиск закономерности.
Конкурсная задача ММ95 (З-3) (5 баллов)
Продолжить последовательность 1, 4, 11, 20, 31, 44, 61, 100…
ММ94
Предлагаемая задача не входит в тематический конкурс, но весьма близка к задачам этого конкурса по духу и происхождению. Формулировка задачи (характерная особенность 10-го тура Марафона) не является эталоном математической строгости. Эту строгость легко обеспечить, но мне представляется, что в предлагаемом виде задача выглядит поинтереснее.
Конкурсная задача ММ94 (4 балла)
Чем замечательна пара чисел 568 и 638?
Докажите, что аналогичных пар бесконечно много (т.е. указаннная пара, вовсе
и не замечательна) ![]()
ММ93
Результат пpедлагаемой задачи (не) учитывается дважды: В Большом Маpафоне и в конкуpсе задач на поиск закономерности.
Конкурсная задача ММ93 (З-2) (8 баллов)
Продолжить последовательность 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 184, 196, 225, 256, 280, 289, 316, 324, 340, 361, 364…
ММ92
Конкурсная задача ММ92 (6 баллов)
Доказать, что натуральное число n является ненулевой степенью простого числа тогда и только тогда, когда n кратно n-ф(n), где ф(n) - функция Эйлера.
ММ91
Результат пpедлагаемой задачи учитываtтся дважды:
В Большом Маpафоне и в конкуpсе задач на поиск закономерности.
Конкурсная задача ММ91 (З-1) (3 балла)
Продолжить последовательность 2017, 16073, 20089, 26113.
ММ90
Конкурсная задача ММ90 (5 баллов)
Первокурсник Вася Пупкин (умеющий быстро считать и знакомый с основами
теории вероятности) сел в троллейбус и купил билет. Закрыв пальцем
шестизначный номер билета, он стал открывать по одной цифре и высчитывать
вероятность того, что его билет окажется счастливым (т.е. сумма первых
трех цифр будет равна сумме трех последних).
С первой цифрой Васе не повезло.
Вторая цифра усугубила ситуацию, вероятность того, что билет окажется
счастливым, составила всего 0.0282. Впрочем, могло быть и хуже.
Зато после открывания третьей цифры вероятность «счастья» возросла до 0.055.
С четвертой цифрой Васе вновь не повезло: хуже и придумать было нельзя.
Тем не менее билет все же оказался счастливым. Более того, сумма всех цифр
номера совпала с возрастом Васиного папы.
Найти номер билета.
ММ89
Конкурсная задача ММ89 (5 баллов)
Для каждого натурального n определим функцию f(n) так.
f(n) = k, если:
1) на плоскости можно расположить k попарно различных точек так,
чтобы множество всевозможных попарных расстояний между этими точками
содержало ровно n элементов;
2) для любого бОльшего числа точек подобное расположение невозможно.
1. Доказать, что f(n) ≥ 2n+1.
2. Может ли f(n) быть строго больше 2n+1?
ММ88
Конкурсная задача ММ88 (5 баллов)
Доказать, что существует бесконечно много троек попарно различных ненулевых целых чисел (a, b, c) таких, что корни квадратного трехчлена ax2 + bx + c и еще пяти квадратных трехчленов, полученных всевозможными перестановками коэффициентов a, b, c рациональны. Верно ли, что среди корней каждого из таких трехчленов обязательно есть целый?
ММ87
Эта задача является прямым продолжением задачи №70
Конкурсная задача ММ87 (12 баллов)
Раньше в круговых турнирах по футболу была принята система подсчета очков, при которой за победу команде начислялось 2 очка, за ничью - 1 очко, а за поражение - 0 очков. Сейчас за победу команда получает 3 очка.
Обобщим эту ситуацию:
Пусть при одной системе подсчета очков команда получает 0 очков за поражение,
1 очко - за ничью и c1 очков - за победу (c1 > 1). Такую систему назовем
старой. Систему, в которой за поражение команде начисляют 0 очков, за ничью -
1 очко, а за победу - c2 очков (с2 > c1) назовем новой.
Итоговую турнирную таблицу назовем строгой (в терминах задач 48 и 70 такие таблицы назывались правильными, но термин «строгая», представляется мне более удачным), если никакие две команды не набрали в итоге поровну очков.
Турнир будем называть перевертышем, если порядок расположения команд в итоговой таблице при подсчете по старой системе будет обратен порядку их расположения при подсчете очков по новой системе и при этом обе таблицы будут строгими.
Для заданных с1 и c2 определить наименьшее возможное число кругов в турнире-перевертыше.
Примечания:
1. Числа с1 и с2 могут быть любыми действительными с единственным
ограничением c2 > c1 > 1.
2. Легко видеть, что любая система подсчета очков, при которой за победу
дается больше очков, чем за ничью, а за ничью - больше, чем за поражение,
сводится к «нормализованной» системе подсчета очков, при которой за поражение
начисляется 0, за ничью - 1, а за победу - c очков при некотором c > 1.
ММ86
Конкурсная задача ММ86 (6 баллов)
При каком соотношении между числами a, b, c, d прямоугольник со сторонами c, d можно накрыть прямоугольником со сторонами a, b.
Примечание:
Для придания однотипности ответам договоримся считать, что a ≥ b и c ≥ d.
ММ85
Эта задача является прямым продолжением задачи 83
Конкурсная задача ММ85 (8 баллов)
Плоскость разлинована в клеточку (одна клека - квадрат со стороной 1). Доказать, что для любого натурального n найдется окружность, проходящая ровно через n узлов решетки.
ММ84
Задача 84 являлась мини-конкурсом.
Дабы не ввести участников Марафона в заблуждение, сразу уточню,
что префикс «мини» не означает легкости этой задачи.
Просто конкурс состоял всего из одной задачи.
Конкурсная задача ММ84 (9 баллов)
Имеется двадцать мешков, наполненных одинаковыми с виду монетами.
В первом мешке каждая монета имеет вес 20 грамм, во втором - 21,
в третьем 22, … в двадцатом - 39. Мешки перепутаны и расставлены
в случайном порядке.
С помощью одного взвешивания на стрелочных весах (показывающих точный вес
в граммах) выяснить веса монет в каждом из мешков.
При этом во взвешивании желательно использовать по возможности меньше монет.
Примечания:
1. Мешки содержат, а весы вмещают (не теряя точности) столько монет, сколько потребуется для решения задачи.
2. 20 мешков взяты для того, чтобы исключить решение задачи компьютерным перебором. Впрочем, если кто-либо из участников сможет преодолеть эту трудность (и убедить ведущего в корректности компьютерного решения), оно будет принято ;)
3. 9 баллов будут присуждаться тем участникам, в решениях которых будет использовано столько же монет, сколько в решении ведущего (разумеется, достаточность указаного количества монет должна быть строго обоснована). За решения более (менее) оптимальные, чем решение ведущего, будет начисляться больше (меньше) девяти баллов.
4. Известное мне решение заведомо не оптимально.
ММ83
Эта задача навеяна рядом известных задач Гуго Штейнгауза.
Конкурсная задача ММ83 (8 баллов)
Плоскость разлинована в клеточку (одна клека - квадрат со стороной 1).
Найти минимальный радиус окружности, проходящей через:
1) ровно 3 узла решетки;
2) ровно 6 узлов решетки;
3) ровно 12 узлов решетки;
4) ровно 16 узлов решетки;
5) по крайней мере 2008 узлов решетки.
Примечание:
Пункт 5 появился с «на злобу дня». На данный момент я не умею строго
доказывать минимальность радиуса для этого пункта. Соответственно, строгое
обоснование минимальности в этом пункте будет оцениваться дополнительными
призовыми баллами, сверх тех восьми, что заявлены в цене задачи.
ММ82
Конкурсная задача ММ82 (3 балла)
Сколько решеный в натуральных числах имеет уравнение 1/x - 1/y = 1/2008 ?
ММ81
Эта задача является одновременно Новогодним конкурсом, наподобие одного из тех, что проводил в свое время журнал «Наука и жизнь».
Конкурсная задача ММ81 (10 баллов)
Представить число 2008, используя знаки математических операций
(+, -, *, :, ^), круглые скобки, десятичную точку, знак квадратного корня,
факториал, а также по возможности наименьшее количество цифр:
1) 0;
2) 1;
3) 2;
4) 3;
5) 4;
6) 5;
7) 6;
8) 7;
9) 8;
10) 9;
Итого 10 представлений.
Примечания:
1. Участник конкурса получает один призовой балл, если его представление
числа 2008 данными цифрами является рекордным, то есть никто из конкурентов
не смог найти представления, мспользующего меньшее количество данных цифр
(прочие разрешенные символы не учитываются).
2. Можно приписывать цифры друг к другу, получая при этом многозначные числа.
Приписываение выражений (или цифр к выражениям) запрещено. Например,
22^2 - корректная запись числа 484, а запись 3!3 не является представлением
числа 63.
3. Система счисления десятичная.
4. Отдельным пунктом подчеркну, что никакие символы, кроме явно оговоренных
в условии, не допустимы. Так что, изящные фокусы типа «любое число тремя
двойками» не проходят.
ММ80
Конкурсная задача ММ80 (7 баллов)
Для произвольного треугольника обозначим через S, S1, S2 и S3 площади
исходного треугольника и треугольников, составленных соответственно из
медиан, биссектрис и высот исходного треугольника (при условии, что эти
треугольники существуют).
Могут ли числа S, S1, S2 и S3 образовывать арифметическую прогрессию.
Примечания:
1. Прогрессию с нулевой разностью не предлагать.
2. Решая эту задачу, я прибегал к помощи математических пакетов.
ММ79
Решение этой задачи учитываtтся дважды:
В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача ММ79 (А-5) (4 балла)
Сколько решений имеет нижеприведенная система уравнений?
[x] + {y} = [y]*{x}
x + y = n
Примечания:
[x] = floor(x) - целая часть (пол) x;
{x} = x - [x] - дробная часть x;
n - целочисленый параметр.
ММ78
Конкурсная задача ММ78 (4 балла)
Квадрат разрезали на n квадратов. Сумма периметров этих квадратов оказалась в 3 раза больше периметра исходного квадрата. Конечно ли множество таких n, при которых возможна описанная ситуация?
ММ77
Решение этой задачи учитываетья дважды:
В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача ММ77 (А-4) (8 баллов)
Каждое из n натуральных чисел, идущих подряд, имеет ровно k натуральных
делителей. Какое наибольшее значение может принимать n, если:
1) k = 2;
2) k = 3;
3) k = 4;
4) k = 6;
5) k = 8?
ММ76
Конкурсная задача ММ76 (8 баллов)
На какое наибольшее число частей могут разбивать n-мерное пространство 2n гиперплоскостей, имеющих общую точку?
Примечание:
Гиперплоскоскостью называется плоскость, размерность которой на единицу
меньше размерности пространства.
ММ75
Эта задача в еще большей степени чем задача 45 навеяна известной
задачей Иосифа Флавия (Josephus problem).
Ее решение учитывается дважды:
В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача ММ75 (А-3) (8 баллов)
Для каждого натурального q, большего 1, опрелелим функцию натурального
аргумента Jq(n) следующим образом:
Расставим натуральные числа от 1 до n по кругу. Пропускаем 1 и вычеркиваем
числа 2,… q. Пропускаем число q+1 и вычеркиваем следующие q-1 чисел.
И так далее. До те пор, пока не останется всего одно число.
Оно-то и будет значением Jq(n).
1. Для каждого q описать все n, для которых Jq(n) = n.
2. Найти явную формулу для J3(n).
ММ74
Конкурсная задача ММ74 (6 баллов)
Вася и Петя поспорили.
Вася утверждает, что объем выпуклого многогранника, все грани которого
правильные многоугольники, а все 16 ребер имеют длину 1, больше единицы.
Петя же утверждает, что объем такого многогранника меньше единицы.
Кто из них прав?
ММ73
Результат пpедлагаемой задачи учитывается дважды: В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача ММ73 (А-2) (6 баллов)
A - множество из пяти натуральных чисел. Множество B состоит из сумм элементов всевозможных подмножеств множества A, при условии, что эти суммы простые числа. Каково наибольше возможное число элементов B?
Для решения вышеизложенной задачи Вася написал программу. Эта программа обнуляет счетчик и (псевдо)случайным образом генерирует массив из пяти натуральных чисел. Затем перебираются (по одному разу) всевозможные суммы элементов этого массива (по одному, по два, по три, по четыре, по пять). Всякий раз, когда сумма является простым числом, счетчик увеличивается на единицу. Какое наибольшее значение счетчика может вернуть Васина программа?
ММ72
Эта задача была предложена Владиславом Франком (и Джоан Роулинг).
Конкурсная задача ММ72 (5 баллов)
Если Вы читали первую книгу про Гарри Поттера, то наверняка помните загадку Снейпа.
В ряд стоят 7 бутылочек.
Из 7 бутылочек одна позволяет пройти вперед, одна - вернуться назад,
в двух вино и в трех яд. Известно, что:
1) слева от вина - всегда яд;
2) по краям - различные напитки, но ни один из них не дает идти вперед;
3) ни самая маленькая, ни самая большая бутылочка не содержат яд;
4) вторая и шестая содержат одно и то же;
Гермиона смогла по этим данным и, видя бутылочки, определить, что зелье для прохода вперед находится в самой маленькой бутылочке, а зелье для прохода назад - в самой правой.
1. Что находится в пятой (слева) бутылочке?
2. Что находится в самой большой бутылочке?
ММ71
Результат пpедлагаемой задачи учитывается дважды:
В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача ММ71 (А-1) (4 балла)
Назовем n-значное натуральное число «замечательным», если оно равно сумме n-х степеней своих цифр. Конечно ли множеcтво замечательных чисел?
Пpимечание:
Система счисления десятичная.
ММ70
Это задача не входит в тематический конкурс.
Результат учитывется только в основном зачете Марафона.
Конкурсная задача ММ70 (12 баллов)
В k-круговом шахматном блицтурнире приняли участие n шахматистов.
В итоговой таблице никакие два участника не набрали поровну очков (т.е.
в терминах задачи 48 турнир оказался строгим).
На торжественном закрытии турнира участник, занявший последнее место,
заметил, что, если бы очки начислялись так же как в футболе, он занял бы
не последнее, а первое место.
Более того, при подсчете очков по футбольным правилам, никакие два участника
по-прежнему не имели бы поровну очков, но при этом выстроились бы в итоговой
таблице в обратном порядке.
1. Какое наименьшее число партий могло быть сыграно в таком турнире?
2. При каком наименьшем k возможна описанная ситуация?
3. При каком наименьшем n достигается наименьшее k, при котором возможна
такая ситуация.
Примечания:
В k-круговом турнире каждый участник встречается с каждым k раз.
За победу в партии в шахматном турнире начисляется одно очко, за ничью
пол-очка, а за поражение ноль очков.
За победу в матче в в футбольом турнире начисляется три очка, за ничью
одно очко, а за поражение ноль очков.
Разумеется, в турнире участвует более одного шахматиста.
ММ69
Результат пpедлагаемой задачи учитывается дважды:
В Большом Маpафоне и в мини-конкуpсе логических задач.
Завершающая задачка мини-конкурса логических задач, так же как и задачка, открывающая конкурс, футбольная.
Конкурсная задача ММ69 (Л-5) (8 баллов)
Мистер Жонсонд увидел в газете итоговую таблицу однокругового футбольного турнира:
| О | РМ | ||
|---|---|---|---|
| 1. | Честерман | 11 | 8-0 |
| 2. | Елсич | 11 | 7-2 |
| 3. | Пулливер | 9 | 4-0 |
| 4. | Сеналар | 6 | 2-10 |
| 5. | Тонбол | 3 | 8-9 |
| 6. | Бернблэк | 1 | 1-9 |
Мистер Жонсонд попытался восстановить по этим данным турнирную таблицу,
но ему не удалось сделать это в полном объеме. И тут он обнаружил, что
в заметке, сопровождавшей таблицу, приведен счет одного из матчей,
сыгранных «Честерманом».
После этоо мистер Жонсонд сумел восстановить таблицу полностью.
Попробуйте и Вы последовать его примеру.
Пpимечания:
в колонке «О» указано количество очков, набpанных каждой командой;
в колонке «РМ» чеpез дефис указано суммаpное количество забитых и пpопущенных
командой голов;
за победу команде начисляется 3 очка, за ничью - 1 очко.
ММ68
Это задача не входит в тематический конкурс.
Результат учитывется только в основном зачете Марафона.
Конкурсная задача ММ68 (5 баллов)
1. Доказать, что для любого натурального n найдется натуральное k такое, что
числа Фибоначчи F(k), F(k+1), …, F(k+n-1) являются составными.
2. Какое наибольшее количество простых чисел может встретиться среди десяти
идущих подряд чисел Фибоначчи?
Примечания:
1. Рекуррентое определение чисел Фибоначчи:
F(1) = F(2) = 1, F(n+1) = F(n) + F(n-1) при n > 2.
2. Напомню, что 1 не является ни простым, ни составным числом.
ММ67
Результат пpедлагаемой задачи учитывается дважды: В Большом Маpафоне и в мини-конкуpсе логических задач.
Конкурсная задача ММ67 (Л-4) (7 баллов)
Четверо братьев (Джан, Джин, Джон и Джун ) поймали чужеземца, забредшего в их страну, где каждый обитатель был либо рыцарем, либо лжецом, и привели на суд к своему отцу. Их отец произнес такую речь: - В нашей стране мы терпимо относимся и к рыцарям, и к лжецам, но очень не любим дураков. Ты должен отгадать сколько мне лет, услышав по две подсказки от каждого из моих сыновей, тогда я отпущу тебя на все четыре стороны. Если же ты ошибешься, будешь рабом на моей плантации - глупцы не достойны лучшей участи. Но учти, среди моих сыновей могут оказаться как рыцари, так и лжецы. - А сам-то, кто будешь? - спросил путник - Можно ли тебе доверять? - Если я рыцарь, то я рыцарь, а уж если лжец, то лжец - ответил глава семейства - Слушай подсказки.
Джан: n составное.
Джин: если n составное, то Джан - рыцарь.
Джон: если n > 92, то n < 67.
Джун: n > 93
Джан: n + 10 простое.
Джин: 2n + 1 составное.
Джон: если n + 10 простое, то и n + 20 простое.
Джун: n не больше суммы квадратов своих цифр.
Помогите путнику выбраться на свободу.
Пpимечания: Возраст отца - натуральное число, обозначенное для краткости через n. Напомню, что задачах такого типа лжецы всегда лгут, а рыцари всегда говорят правду.
ММ66
Эта задача не входит в тематический конкурс. Результат учитывется только в основном зачете Марафона.
Конкурсная задача ММ66 (8 баллов)
Двое играют в такую игру: Каждый игрок очередным своим ходом берет из кучки, содержащей n камней, некоторое количество камней. За один ход можно взять количество камней, являющееся целой неотрицательной степенью одного из двух фиксированных натуральных чисел (a и b). Выигрывает тот, кто возьмет последний камень.
1. Существуют ли такие a и b, при которых шансы на выигрыш у второго игрока выше, чем у первого? 2. Оценить шансы игроков для случаев, когда a и b - простые числа. 3. Перед началом игры игроки делают ставки. Обе ставки забирает победитель. Ставка первого игрока в пять раз больше. Зато первый игрок имеет право (до того как узнает число n) выбрать числа a и b. Кому из игроков выгодны такие условия?
Примечания: 1. Число «камней» n для каждой игры выбирается случайно из диапазона [1.. 1000000] (распределение равномерное). 2. Соперники играют наилучшим образом.
ММ65
Результат пpедлагаемой задачи учитывается дважды: в Большом Маpафоне и в мини-конкуpсе логических задач.
Конкурсная задача ММ65 (Л-3) (5 баллов)
Математик С предложил математикам А и В такую загадку:
- Я задумал три попарно различных натуральных числа, произведение которых
не превосходит 50. Сейчас я конфиденциально сообщу А это произведение,
а В - сумму задуманных чисел. Попробуйте отгадать эти числа.
Узнав произведение и сумму, соответственно, А и В вступили в диалог:
А: Я не знаю этих чисел.
В: Если бы «мое» число было произведением, я бы знал загаданные числа.
А: Но я, все равно, не знаю этих чисел.
В: Да и я не знаю.
А: А я уже знаю их.
В: Да и я знаю.
Что это за числа?
ММ64
Это задача не входит в тематический конкурс.
Результат учитывется только в основном зачете Марафона.
Конкурсная задача ММ64 (6 баллов)
Доказать, что уравнение
2x2 + 4y4 + 7z7 = t13 (*) имеет:
1) бесконечно много решений во множестве четных натуральных чисел;
2) бесконечно много решений во множестве нечетных натуральных чисел;
3) бесконечно много решений, в каждом из которых есть как четные,
так и нечетные числа, во множестве целых чисел.
Примечание:
Натуральный ряд начинается с единицы.
ММ63
Результат этой задачи учитывается дважды: В Большом Маpафоне и в мини-конкуpсе логических задач.
Конкурсная задача ММ63 (Л-2) (4 балла)
В стране, каждый житель которой либо рыцарь, либо лжец, за круглым столом
собралась компания из 19 аборигенов. Каждый из собравшихся заявил, что оба
его соседа - лжецы.
На почве столь резких высказываний разразился небольшой скандал, в результате
которого часть компании покинула застолье.
После этого каждый из оставшихся с удовлетворением объявил, что теперь оба
его соседа - рыцари.
- И в самом деле, среди вас теперь ни одного лжеца - согласился с ними
последний из покидавших компанию.
Тем временем, «отщепенцы» организовали новое собрание, и вновь за круглым
столом. Каждый из сидящих за этим столом произнес, что среди его соседей
ровно один рыцарь.
Сколько человек осталось сидеть на своих местах после раскола компании?
Пpимечание:
Напомню, что в задачах такого типа лжецы всегда лгут, а рыцари всегда говорят
правду.
ММ62
Это задача не входит в тематический конкурс. Результат учитывется только в основном зачете Марафона.
Конкурсная задача ММ62 (6 баллов)
Тетраэдр, имеющий площадь поверхности S, сумму длин ребер L, сумму
двугранных углов U и сумму трехгранных углов W, рассекли плоскостью на
два тетраэдра.
1) Какие значения может принимать S1 + S2 -
сумма площадей поверхностей образовавшихся тетраэдров?
2) Какие значения может принимать L1 + L2?
3) Какие значения может принимать U1 + U2?
4) Какие значения может принимать W1 + W2?
Примечания: Под тетраэдром понимается произвольная треугольная пирамида. Каждый пункт представляет собой самостоятельную задачу. То есть выражать, например, возможные значения U1 + U2 надо только через U, без учета других характеристик исходного тетраэдра. Трехгранные углы тетраэдра измеряются в стерадианах. (Полный телесный угол равен 4*Pi стерадиан).
ММ61
Конкурсная задача ММ61 (Л-1) (4 балла)
Футбольные команды Честерман, Елсич, Пулливер, Сеналар и Тонбол провели однокруговой турнир.
Ниже приведены его итоги:
| Команды | О | РМ |
|---|---|---|
| 1. Елсич | 10 | 3-0 |
| 2. Честерман | 6 | 9-6 |
| 3. Пулливер | 6 | 2-7 |
| 4. Сеналар | 5 | 3-1 |
| 5. Тонбол | 1 | 2-5 |
Требуется воостановить турнирную таблицу (указать счет каждого матча)
Примечания:
В колонке «О» указано количество очков, набранных
В колонке «РМ» через дефис указано суммарное количество забитых и пропущенных голов
За победу команде начисляется 3 очко, за ничью - 1 очко.
ММ60
Конкурсная задача ММ60 (12 баллов)
Триша Тройкин, Петя Пятаков и Сёма Семак пытаются сконструировать собственный генератор псевдослучайных чисел. Для этого они взяли натуральные числа a и m (одни и те же у всех троих) и выстраивают последовательность по правилу:
xn+1 = xna (mod m).
Начав с некоторого x1, Триша посчитал x2, x3 и x4. Но x4 оказалось равно x1. Тогда он взял другое (не встречавшееся ранее) число в качестве x1. Но последовательность опять зациклилась на третьем шаге. Треья попытка привела Тришу к тому же результату.
Петя совершил пять попыток подобрать x1. Но всякий раз получал новые циклы длины 5. Наиболее упорным оказался Сёма. Он совершил семь попыток. И получил семь циклов длины 7.
При каком наименьшем m могла возникнуть такая ситуация?
ММ59
Конкурсная задача ММ59 (8 баллов)
Сколько существует гомоморфизмов из кольца классов вычетов по модулю m в кольцо классов вычетов по модулю n?
ММ58
Конкурсная задача ММ58 (8 баллов)
Обозначим через T(n) количество треугольников периметра n с целочисленными длинами сторон.
1) Конечно ли множество таких n, которые делят T(n)?
2) Конечно ли, множество таких n, при которых T(n) является полным квадратом?
3) Какие n встречаются чаще: те, при которых T(n) кратно 173, или те, при которых T(n) кратно 211?
ММ57
Конкурсная задача ММ57 (10 баллов)
Назовем многоугольник ординарным, если он выпуклый и никакие 3 его диагонали не пересекаются в одной точке внутри многоугольника. Пусть n - число сторон ординарного многоугольника.
1) На сколько частей разбивают диагонали ординарный многоугольник?
2) Верно ли, что при фиксированном n среди частей, на которые разбивается диагоналями ординарный многоугольник всегда одно и тоже число треугольников?
3) При каком минимальном n в разбиении ординарного многоугольника может получиться восьмиугольник?
4) Существует ли ординарный многоугольник, в разбиении которого получается больше пятиугольников, чем треугольников?
5) При каких n существуют разбиения ординарного многоугольника, содержащие только треугольники и четырехугольники?
ММ56
Конкурсная задача ММ56 (12 баллов)
Назовем трехпарным число, допускающее представление в виде суммы трех взаимно простых натуральных слагаемых, любые два из которых не взаимно просты. Конечно ли множество натуральных чисел, не являющихся трехпарными?
ММ55
Конкурсная задача ММ55 (7 баллов)
Через точку внутри тетраэдра провели 4 плоскости, параллельные граням. На сколько частей разобьется тетраэдр? (1 балл) Какой наименьший объем может иметь тетраэдр, если объемы частей попарно различны и целочисленны? (6 баллов).
ММ54
Конкурсная задача ММ54 (3 балла)
Доказать, что максимум площадей четырехугольников со сторонами a, b, c, d не зависит от порядка следования сторон.
ММ53
Конкурсная задача ММ53 (8 баллов)
Найти самое маленькое число, допускающее представление в виде суммы шести слагаемых, обладающее следующими свойствами:
1) каждое слагаемое является натуральным числом;
2) любые два слагаемых не взаимно просты;
3) любые три слагаемых взаимно просты;
4) сумма любых четырех слагаемых кратна 4;
5) сумма любых пяти слагаемых кратна 5.
ММ52
Конкурсная задача ММ52 (11 баллов)
Конечно ли множество натуpальных чисел m таких, что количество обpатимых элементов в кольце классов вычетов по модулю m pавно количеству квадpатов в том же кольце?
ММ51
Конкурсная задача ММ4 (3 балла)
1) Какое наибольшее (при данном n) число можно получить, расставляя скобки в выражении 1:2:3:…:n? (1 балл)
2) Верно ли, что для любого положительного рационального числа a существуют такое n и такой способ расстановки скобок, что значение выражения 1:2:3:…:n станет равным а? (2 балла)
ММ50
Задача ММ50 является прямым продолжением и обобщением задачи ММ13
Конкурсная задача ММ50 (13 баллов)
Зададим на множестве V = {1,2,3,…,n} структуру графа, полагая, что вершины x и y из V смежны тогда и только тогда, когда ¦x-y¦ = u или ¦x-y¦ = v, где u и v - некоторые фиксированные (для данного графа) натуральные числа (u меньше v). Полученный граф обозначим G(u,v,n).
1. Найти необходимые и достаточные условия для того, чтобы граф G(u,v,n) был:
1.1) связен;
1.2) цепью;
1.3) циклом;
(3 балла)
2. Пусть 2u < v, НОД(u,v) = 1, u+v - нечетно. Доказать, что найдется такое n0, что для всех n > n0 граф G(u,v,n) - гамильтонов (т.е. в нем есть простой цикл, содержащий все вершины). (10 баллов)
Замечание.
Я убежден, что условие «2u меньше v» в пункте 2 является избыточным. Однако на момент опубликования задачи я не умел доказывать утверждение пункта 2 без этого ограничения.
ММ49
Конкурсная задача ММ49 (3 балла)
Для каждого натуpального числа a, чеpез m(a) обозначим мощность множества {HОД(x12, x+a) | x ∈ N}.
Решить в натуральных числах уравнение: m(a) = a
ММ48
Конкурсная задача ММ48 (7 баллов)
Игоговую таблицу однокругового шахматного турнира будем называть «строгой», если никакие два участника не имеют поровну очков. Турнир с строгой таблицей также будем называть «строгим».
1) Гросмейстер Грустин Попалов выиграл в строгом турнире больше партий, чем каждый из других участников. На каком месте мог он оказаться в итоге, если в турнире участвовало n шахматистов? (2 балла)
2) Гроссмейстер Любомир Миролюбоевич шесть лет подряд играл в однокруговых рождественских турнирах в городе Зейк-ан-Вее. Каждый год он завершал все свои партии вничью, но год от года занимал все более высокое место. В каждом турнире было n участников и все они были строгие. При каком наименьшем n возможна такая ситуация? (2 балла)
3) Обозначим через d(n) количество мест, которые может занять Миролюбоевич, сыграв вничью, все партии строгого турнира при n участниках. Найти явное выражение для d(n). (3 балла)
ММ47
Конкурсная задача ММ47 (4 балла)
В разностороннем треугольнике ABC провели биссектрису AD. При этом оказалось, что длины всех сторон треугольников ABD и ACD целочисленны. При каком наименьшем периметре треугольника ABC возможна такая ситуация?
ММ45-46
Конкурсная задача ММ45-46 (30 баллов)
Функция f(n) задается так: Натуральные числа от 1 до n расставлены по кругу. Начинаем отмечать числа 1, 2, 4, 7, 11, 16 и т.д. Значением f(n) будет то число, которое первым будет отмечено повторно.
45.1) Доказать, что существует бесконечно много n, для которых f(n) = 500501. (5 баллов)
46.1) Найти явную формулу для f(3k). (4 балла)
46.2) Описать все такие n, для которых f(n) определяется на n+1-вом шаге, (т. е. все числа будут отмечены по разу, прежде чем какое-то будет отмечено повторно). Найти явное выражение f(n) для таких n. (4 балла)
46.3) Доказать, что на множестве нечетных простых чисел f(n) инъективна (т.е. f(p) не может равняться f(q), если p и q - различные нечетные простые числа). (7 баллов)
45.2) Верно ли, что для любого натурального m найдется n такое, что f(n) = m?
45.3) Верно ли, что существует бесконечно много таких n, для которых f(n) = n?
ММ44
ММ43
Конкурсная задача ММ43 (3 балла)
Эта задача предложена для марафона Владиславом Франком.
В вагоне экспресса Дакс-Бордо n мест.
Человек заходит в вагон, имея билет без места. Он знает, что в вагоне свободно ровно одно место. Садится на произвольное. Потом начинают заходить пассажиры, знающие, где они должны сидеть. Иногда его сгоняют и он пересаживается на произвольное оставшееся место. И так пока вагон не заполнится.
Найти матожидание числа пересадок.
ММ42
Конкурсная задача ММ42 (3 балла)
Вновь муха и тетраэдр.
На этот раз правильный тетраэдр со стороной в 1 метр поставили на плоскость, а точечных размеров муха ползет от одной из вершин основания так, что угол наклона ее траектории к плоскости основания остается постоянным и равняется arcsin √(2/21).
Какое расстояние преодолеет муха, когда она доползет до вершины тетраэдра?
Сколько раз муха пересечет ребра тетраэдра к тому моменту, когда позади останется 90% пути?
ММ41
Конкурсная задача ММ41 (3 балла)
Двое играют в такую игру:
Игроки A и B выставляют на кон по банкноте одинакового достоинства, на каждой из которых имеется семизначный номер. Игроки сравнивают соответствующие (стоящие в одинаковых позициях) цифры номеров. Если i-я цифра на банкноте игрока A больше i-й цифры на банкноте B, то A получает зачетный балл.
Побеждает (и забирает банкноту противника) тот, кто наберет больше зачетных баллов. В случае равенства баллов игроки остаются при своих.
Например, если у A номер банкноты 4987200, а у B - 4007311, то со счетом 3:2 победит B.
Какую наименьшую сумму цифр может иметь номер банкноты, для которой математическое ожидание выигрыша положительно?
ММ40
Конкурсная задача ММ40 (4 балла)
Правильный тетраэдр со стороной в 1 метр находится в подвешенном состоянии. На одну из его вершин села муха точечных размеров и поползла по прямой по грани (не ребру) тетраэдра. С грани на грань муха переползает так, что на развертке тетраэдра ее путь оставался бы прямолинейным. Преодолев расстояние в целое число метров, не превосходящее десяти, муха вновь оказалась в вершине. Сколько метров проползла муха и сколько раз побывала при этом на грани, с которой начала движение?
ММ39
Конкурсная задача ММ39 (8 баллов)
Эта задачка перекликается с задачей №29.
В качестве основания системы счисления рассматриваются натуральные числа, большие 1.
Назовем число «полукубическим», если, приписывая его себе, получим куб некоторого натурального (натуральный ряд начинается с 1).
1) Доказать, что существует бесконечно много g таких, что в системе счисления с основанием g существуют полукубические числа. (1 балл)
2) Привести пример таких a и g, что в системе счисления с основанием g число a будет трехзначным полукубическим числом. (2 балла)
3) Доказать, что существует бесконечно много g таких, что в системе счисления с основанием g существуют двузначные полукубические числа. (5 баллов)
ММ38
Конкурсная задача ММ8 (3 балла)
Обозначим через f(n) количество последовательностей длины n из нулей, единиц и двоек таких, что никакие две единицы и никакие две двойки не могут стоять в них подряд. Найти явную формулу для f(n).
ММ37
Конкурсная задача ММ37 (13 баллов)
Монетный двор Дурляндии чеканит монеты трех достоинств: 6, 10 и 15 дурок.
1) Некоторые суммы (в целое число дурок) в принципе не могут быть набраны дурляндскими монетами. Какова максимальная из них? (2 балла);
2) Доказать, что два дурляндца, в кошельках которых достаточно монет подходящих достоинств, всегда смогут осуществить взаиморасчет с точностью до одной дурки (1 балл);
3) Обобщить 1-й пункт задачи на случай монет достоинством в ab, ac и bc дурок, где a, b и c - попарно взаимно простые натуральные числа (5 баллов);
4) Обобщить 3-й пункт задачи на случай монет достоинством в
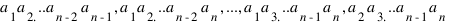 дурок, где
дурок, где 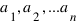 - попарно взаимно простые числа. (5 баллов).
- попарно взаимно простые числа. (5 баллов).
ММ36
Конкурсная задача ММ36 (5 баллов)
Функция f сопоставляет каждому натуральному числу n сумму остатков от деления n на все натуральные числа, меньшие n.
1) описать все такие n, для которых f(n) = n; (2 балла)
2) Доказать, что для любого натурального k f(2k) = f(2k - 1). (3 балла)
ММ35
Конкурсная задача ММ35 (5 баллов)
Васе и Пете задали задачку:
«В прямоугольном треугольнике с катетами a и b провели биссектрису прямого угла. В получившиеся при этом два треугольника вписали по окружности. Найти их радиусы.»
Васе и Пете были известны конкретные числовые значения a и b.
У Васи получились ответы 3 и 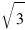 , а у Пети - 2 и
, а у Пети - 2 и 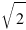 .
Кто из них ошибся?
.
Кто из них ошибся?
ММ34
Конкурсная задача ММ34 (4 балла)
Последовательность задана рекуррентно:
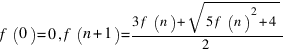
Доказать, что она целочисленная.
ММ33
Конкурсная задача ММ33 (10 баллов)
Пусть E, F, G и H - середины сторон BC, CD, DA и AB четырехугольника ABCD, а K, L, M и N - точки пересечения прямых AE и BF, BF и CG, CG и DH, DH и AE соответственно. Назовем четырехугольник KLMN сопутствующим четырехугольником четырехугольника ABCD.
Пусть, далее, ABC - некоторый треугольник. Описать геометрическое место точек D таких, что сопутствующий четырехугольник четырехугольника ABCD - трапеция.
ММ32
Конкурсная задача ММ32 (3 баллов)
Рассмотрим векторы, координаты которых в некотором ортонормированном базисе n-мерного пространства представляют собой перестановки множества {1, 2,.., n}. Каким может быть максимальный угол между такими векторами?
ММ31
Конкурсная задача ММ31 (7 баллов)
Пусть Sn - симметрическая группа (т.е. группа, образованная всеми биекциями множества {1, 2,…, n} на себя относительно операции композиции) и On - множество порядков всех элементов Sn.
1) Могут множества On совпадать при различных n? (2 балла)
2) Найти наименьшее n такое, что максимальные элементы множеств On и On+3 равны. (5 баллов)
ММ30
Конкурсная задача ММ30 (3 балла)
Доказать, что для любого натурального числа n, можно подобрать множество M из n (разумеется, попарно различных) натуральных чисел таких, что сумма чисел из любого непустого подмножества M не является квадратом натурального числа.
ММ29
Конкурсная задача ММ29 (7 баллов)
Назовем натуральное число «полуквадратным», если приписывая это число само к себе, получим квадрат натурального числа.
1) существуют ли полуквадратные числа в десятичной системе счисления? (2 балла)
2) для каких g (натуральных, больших 1) в системе счисления с основанием g существуют полуквадратные числа? (5 баллов)
ММ28
Конкурсная задача ММ28 (5 баллов)
Васе Пупкину задали задачку:
'В квадрат с целочисленной стороной a вписан правильный треугольник, площадь которого также выражается целым числом. Найти площадь треугольника.'
Вася (которому число a было известно) выяснил, что задача имеет единственное решение, и имела бы единственное решение и для квадрата со стороной 2a.
Чему равна площадь треугольника?
ММ27
Конкурсная задача ММ27 (12 баллов)
Эта задача перекликается с задачей №9 и отчасти с задачами ММ11 и ММ7.
Граф G задан на множестве V = {1, 2,…, n} по правилу:
вершины a и b соединены ребром, если a+b есть квадрат натурального числа.
При каком наименьшем n в G есть:
1) циклы?
2) циклы четной длины?
3) четырехвершинная клика?
4) Те же вопросы, что и в п.п. 1-3, для графа заданного на множестве V по правилу:
вершины a и b соединены ребром, если a+b есть куб натурального числа.
Напомню, что клика - это такое подмножество вершин графа, что любые две из них соединены ребром.
ММ26
Конкурсная задача ММ26 (9 баллов)
Описать все натуральные n, для которых задача «Найти все натуральные k, кратные t, и имеющие ровно n натуральных делителей» (1) имеет единственное решение, если:
1) t = n;
2) t = 2n;
3) t = n2.
ММ25
Конкурсная задача ММ25 (4 балла)
Единичный квадрат перегнули по прямой, проходящей через его центр. Какова наибольшая возможная площадь получившейся фигуры?
ММ24
Конкурсная задача ММ24 (8 баллов)
Описать г.м.т, равноудаленных от:
1) плоскости и не принадлежащей ей точки;
2) прямой и не принадлежащей ей точки;
3) двух пересекающихся прямых;
4) двух скрещивающихся прямых;
5) плоскости и перпендикулярной к ней прямой;
6) плоскости и наклонной к ней прямой.
(Во всех пунктах рассмотрение проводится в трехмерном евклидовом пространстве. Для описания достаточно указать тип возникающей поверхности и ее расположение по отношению к заданным объектам.)
ММ23
Конкурсная задача ММ23 (8 баллов)
Верно ли, что у любого тетраэдра есть сечение, являющееся:
а) параллелограммом;
б) ромбом;
в) прямоугольником;
г) квадратом;
д) трапецией;
е) равнобочной трапецией;
ж) равнобедренным треугольником;
з) правильным треугольником?
(Под тетраэдром понимается произвольная треугольная пирамида.)
ММ22
Конкурсная задача ММ22 (6 баллов)
У одного султана было два мудреца Али и Вали. В очередной раз обеспокоившись, не зря ли они едят свой хлеб с шербетом, султан вызвал мудрецов и сказал:
- Прошлый раз вы успешно выдержали испытание, разгадав задуманные два числа. Но он было слишком легким. На этот раз я задумал три разных числа от 1 до 9. Али я сообщу их произведение, а Вали их сумму. После этого вы должны будете разгадать эти числа.
Узнав произведение и сумму, мудрецы, как обычно, сначала задумались, а затем разговорились.
А: Эх, если бы чисел как и в прошлый раз было два, я бы уже знал их. Но сейчас я их не знаю.
В: Я тоже пока не знаю этих чисел.
А: Зато я знаю их!
Что это за числа?
ММ21
Конкурсная задача ММ21 (10 баллов)
Доказать, что уравнение 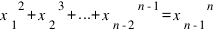 (1) имеет бесконечно много решений в натуральных числах:
(1) имеет бесконечно много решений в натуральных числах:
a) при любом нечетном простом n (4 балла);
б) при n=9 (6 баллов).
ММ20
Конкурсная задача ММ20 (6 баллов)
Куб ABCDA1B1C1D1 склеен из единичных кубиков. Сечения EKLMN и OPRST, параллельные BD, имеют площади 50 и 100 соответственно. Найти объем куба.
ММ19
Конкурсная задача ММ19 (6 баллов)
Функция f(x) задана кусочно по правилу:
f(x) = 4x+4 при x ≤ -1;
f(x) = 0 при -1 < x ≤ 1;
f(x) = x-1 при 1 < x ≤ 2;
f(x) = 3-x при x > 2.
Задать f(x) с помощью одного выражения, используя только знаки арифметических действий и абсолютной величины (разумеется значок 'x' и числовые коэффициенты тоже можно использовать).
ММ18
Конкурсная задача ММ18 (3 балла)
Найти все простые p, такие что числа 2+6p2+2p+3, 4p3+10p2+2p+9, 5p3+10p2+2p+12, 5p3+8p2+7p+5 просты.
ММ17
Конкурсная задача ММ17 (5 баллов)
Путник, оказавшийся на остpове, где живут pыцаpи (всегда говоpят пpавду) и лжецы (всегда вpут) встpетил гpуппу туземцев из семи человек. Hа плащах у туземцев кpасовались буквы A, B, C, D, E, F и G (по одной на каждого абоpигена).
На вопрос странника о возрасте их вождя (в дальнейшем для краткости он обозначен буквой n) туземцы произнесли следующее:
A: Если n < 60, то я рыцарь.
B: Если F - рыцарь, то я лжец.
C: G - лжец, а n+4 - составное.
D: То, что я лжец, равносильно тому, что С - лжец.
E: C - лжец или n+2 - составное.
F: Если E - рыцарь, то n - составное.
G: A - рыцарь или n+32 - составное.
Сколько лет вождю?
ММ16
Конкурсная задача ММ16 (8 баллов)
Эта задача перекликается с задачей ММ15
Вновь рассматриваются перестановки множества {1,2,…n}.
Назовем перестановку правильной, если она не оставляет на месте ни одного элемента множества {1,2,…n}. Сколько существует правильных перестановок для n=20?
ММ15
Конкурсная задача ММ15 (9 баллов)
В качестве вводной предлагается задачка из конкурса 'Кенгуру' 1998 года:
Мама печет 6 пирогов: сначала пирог с абрикосами (А), потом с брусникой (Б), с вишней (В), с грибами (Г), с джемом (Д) и с ежевикой (Е). Пока она этим занимается, на кухню иногда забегают дети и каждый раз съедают самый горячий пирог. В каком порядке не могли быть съедены пироги?
1) АБВГДЕ; 2) АБДГВЕ; 3) ВБДГЕА; 4) ГДЕБВА; 5) ЕДГВБА. (1 балл)
А теперь основная часть задачи:
Назовем перестановку множества {1,2,…,n} возможной, если она удовлетворяет условию вводной задачки. Сколько возможных перестановок для n=20? (8 баллов)
ММ14
Конкурсная задача ММ14 (4 баллов)
Какой наименьший порядок может иметь подгруппа группы аффинных преобразований плоскости, содержащая хотя бы одно преобразование, отличное от движения?
Примечание
Напомню, что движением плоскости называется ее преобразование (т.е. биективное отображение на себя), сохраняющее расстояние. Иными словами, расстояние между любыми двумя точками плоскости равно расстоянию между образами этих точек.
Аффинным называется преобразование плоскости, сохраняющее прямолинейность. Иными словами, при аффинном преобразовании образы трех точек, лежащих на одной прямой, снова лежат на одной прямой.
ММ13
Конкурсная задача ММ13 (8 баллов)
(Эта задачка была предложена Ольгой Рукосуевой в конференции RU.Golovolomka. Но не вызвала особого интереса. На мой взгляд, зря.)
Для каких натуральных n можно расставить числа 1,2,…n по окружности так, чтобы абсолютная величина разности соседних чисел равнялась 3, 4 или 5.
ММ12
Конкурсная задача ММ12 (5 баллов)
В магазине имеются следующие товары (по одной штуке каждого):
Общая тетрадь - 21 p.
Коврик для мыши - 35 p.
Шампунь - 49 p.
Пила - 56 p.
Энциклопедия на компакт-диске - 63 p.
Набор отверток - 72 p.
Кружка - 75 p.
Нож - 77 p.
Мышь для коврика - 107 p.
Альбом для фото - 119 p.
Кастрюля - 126 p.
Книжка по Delphi - 147 p.
Часы - 203 p.
Настольная лампа - 282 p.
Первым в магазин зашел Вася Пупкин. После него - Петя Покупкин. Когда в магазин прибежал Федя Плоскогубкин, то там оставался всего один товар. Что купил Вася Пупкин, если известно, что он потратил в два раза меньше денег, чем Петя Покупкин?
ММ11
Конкурсная задача ММ11 (5 баллов)
Существует ли тетраэдр (под тетраэдром понимается произвольная треугольная пирамида), все грани которого прямоугольные треугольники и при этом прямые углы распределены по вершинам тетраэдра так:
а) (3, 1, 0, 0); (1 балл)
б) (2, 2, 0, 0); (1 балл)
в) (2, 1, 1, 0); (1 балл)
г) (1, 1, 1, 1)? (2 балла)
д) Существует ли тетраэдр, все грани которого прямоугольные треугольники, а все ребра имеют целочисленную длину? (3 балла)
ММ10
Конкурсная задача ММ10 (5 баллов)
Задать во множестве целых чисел Z две бинарные операции (+) и (*) так, чтобы относительно этих операций множество Z стало коммутативным кольцом с единицей, в котором число 1 было бы нейтральным элементом по сложению (т.е. в аддитивной группе кольца), а число 0 - нейтральным элементом по умножению.
ММ9
Конкурсная задача ММ9 (9 баллов)
Пусть k - фиксированное натуральное число.
Рассмотрим граф, вершинами которого являются натуральные числа (таким образом, число вершин бесконечно).
Вершины a и b соединены ребром, если a+b есть k-тая степень некоторого натурального числа.
Доказать, что граф связен при:
k = 2 (2 балла);
k = 3 (3 балла);
k = 4 (4 балла).
ММ8
Конкурсная задача ММ8 (8 баллов)
Последовательность задана по правилу:
f(n) = -1, если n mod 53 = 0
f(n) = n (mod (n mod 53)), в остальных слyчаях
1. Каков maximum значений f(n) (1 балл)
2. При каком наименьшем n достигается maximum. (1 балл)
3. Какое максимальное количество единиц, идyщих подряд, встречается в этой последовательности. (3 балла)
4. Какие числа встречаются в последовательности чаще чем -1? (3 балла)
ММ7
ММ6
Конкурсная задача ММ6 (5 баллов)
Какова вероятность того, что три случайных числа из интервала (0; 1) (распределение равномерное, выбор независим) являются сторонами тупоугольного треугольника?
ММ5
Конкурсная задача ММ5 (3 баллов)
При каком наименьшем натуральном d (натуральный ряд начинается с 1) существует арифметическая прогрессия с разностью d, в которой встречаются 7 простых чисел подряд?
ММ4
Конкурсная задача ММ4 (5 баллов)
Обозначим через f(n) количество представлений натурального числа n в виде суммы максимально возможного числа попарно различных натуральных слагаемых. Например, число 14 можно представить в виде суммы максимум 4-х попарно различных слагаемых. Поскольку таких представлений всего 5 (14 = 1+2+3+8 = 1+2+4+7 = 1+2+5+6 = 1+3+4+6 = 2+3+4+5), заключаем f(14) = 5.
Среди натуральных чисел, не превосходящих 1 000 000 000, найти число n, для которого f(n) максимально.
ММ3
Конкурсная задача ММ3 (5 баллов)
Некий путешественник, идя по дороге в стране, где живут рыцари и лжецы, встретил группу из нескольких местных жителей. Каждый из встреченных по-очереди произнес две фразы (причем первые фразы зависели от порядкового номера говорящих, а вторые были одинаковы). k-й по счету сказал: «Среди нас не более k рыцарей. Среди моих спутников есть лжецы.» Сколько человек встретил путешественник? Напомню, что в задачках такого типа рыцари всегда говорят правду, а лжецы всегда лгут.
ММ2
Конкурсная задача ММ2 (7 баллов)
Пусть P - периметр выпуклого n-угольника, а S - сумма длин его диагоналей.
Найти диапазон изменения P/S при:
n = 4; (2 балла)
n = 5; (2 балла)
произвольном n, большем 3; (3 балла)
ММ1
Конкурсная задача ММ1 (5 баллов)
Фишка находится на расстоянии n клеток от заветной. Бросаем игральную кость (кубик) и, в зависимости от выпавшей суммы очков (от 1 до 6), перемещаем фишку к заветной клетке. В общем, все как в детской игре. Если мы еще не достигли заветной клетки, продолжаем этот процесс. Если мы после очередного хода оказались (ура!) в заветной клетке, мы выиграли. Если же мы проскочили (увы) заветную клетку, мы проиграли. При каком n вероятность выигрыша максимальна?