| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Математический марафон
Продолжается 22-й конкурс в рамках Математического марафона
Старожилы Марафона, наверняка, обратили внимание, что привычное слово «тур» заменено на «конкурс». Это сделано, чтобы подчеркнуть самостоятельность этого соревнования.
В связи с этим и рядом других накопившихся изменений в правила Марафона внесены некоторые уточнения.
22-й конкурс - тематический. Во всех задачах тура, кроме ММ216, речь пойдет о выпуклых многогранниках. Во всех задачах, где речь идет о многогранниках, под словом «многогранник» подразумевается выпуклый многогранник.
Стать участником марафона может любой желающий. Некоторые задачи вполне доступны школьникам. Для решения других требуются знания, выходящие за рамки школьного курса. Одни задачи могут показаться вам интересными, а другие - не очень. На вкус и на цвет…
Но если любите поломать голову над нестандартными задачами, участвуйте, не стесняйтесь.
Жду от вас комментариев марафонских задач, а также пожеланий Марафону. Эта обратная связь позволит сделать Марафон интереснее для вас.
Не забывайте, пожалуйста, присылать вместе с Вашими решениями свои эстетические оценки задач по пятибалльной шкале.
Ведущий Марафона — Vladimir letsko
Текущие задачи
ММ219
Конкурсная задача ММ219 (8 баллов)
Решения принимаются до 22:00 (мск) 29.11.2016
Какое наибольшее количество диагоналей может иметь одиннадцатигранник?
ММ220
Конкурсная задача ММ217 (15 баллов)
Решения принимаются до 17.12.2016
Найти наименьшее v такое, что существует многогранник, имеющий v вершин и 2016 диагоналей, а многогранника, имеющего v+1 вершину и 2016 диагоналей, не существует.
Разбор задач
ММ218
Конкурсная задача ММ218 (5 баллов)
Найти наименьшее возможное количество диагоналей многогранника, имеющего 2017 ребер.
Решение
Привожу решения Владимира Чубанова, Олега Полубасова, Анатолия Казмерчука и Владислава Франка.
Решение Владимира Чубанова
ММ218
Найти наименьшее возможное количество диагоналей многогранника, имеющего 2017 ребер.
Ответ: 1004 диагоналей.
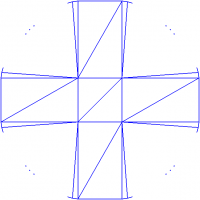
![[img]http://s019.radikal.ru/i600/1611/e3/e8f7633cbe66.png[/img]|рис. 1 [img]http://s019.radikal.ru/i600/1611/e3/e8f7633cbe66.png[/img]|рис. 1](/lib/exe/fetch.php?w=200&tok=5021ba&media=marathon:pic_mm218.png) Пример на 1004 построить легко (см. рисунок). Поставили треугольную призму «домиком» и с одной стороны – со стороны AB – добавили 1004 точки в плоскости ABDF (на рисунке отмечена только часть этих точек). Получили 1008 точек основания и 2 точки «сверху».
Пример на 1004 построить легко (см. рисунок). Поставили треугольную призму «домиком» и с одной стороны – со стороны AB – добавили 1004 точки в плоскости ABDF (на рисунке отмечена только часть этих точек). Получили 1008 точек основания и 2 точки «сверху».
Количество рёбер: 1008+1004+4+1 = 2017;
Количество (пространственных) диагоналей: 1004 – все новые точки соединены с т.E. Других диагоналей нет.
Аргументы в пользу того, что меньше быть не может.
При рассмотрении суммарно всех диагоналей (пространственные + диагонали граней) нетрудно заметить, что наиболее выгодная стратегия лежит не в уменьшении числа вершин и не в разделении вершин по разным граням, а в максимальной консолидации вершин в одной грани-плоскости (поскольку \binom{n}{2} растёт квадратично, при таком количестве точек это перевешивает остальные стратегии).
Поднять только одну вершину над плоскостью недостаточно – количество рёбер будет чётным.
Поднять 2 вершины над плоскостью можно несколькими принципиально разными способами, которые несложно перебрать руками и убедиться, что представленный вариант принадлежит множеству самых выгодных.
Кроме того, приведу и свое решение задачи.
Авторское решение
Я специально не стал заострять внимание на технических деталях, чтобы не скрыть в них основные (довольно простые) идеи.
Пусть многогранник имеет v вершин, e ребер и f граней, а h1,h2, …, f - количества сторон граней. Очевидно, что количество ребер такого многогранника многогранника вычисляется по формуле:
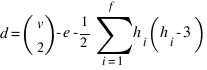 (1)
(1)
Легко видеть, что при фиксированных e и f сумма
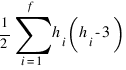
будет тем меньше, чем равномернее распределены значения hi. И, соответственно, тем больше, чем больше самое большое из hi (в дальнейшем будем считать, что это h1.
При четных e h1 может достигать e/2. Этот случай соответствует пирамидам, у которых d=0.
В нашем случае наибольшее значение h1 = 1008 достигается при v = 1010, f = 1009. Соответствующие многогранники (еще две его грани четырехугольны, а остальные треугольны) легко строится. Их изображения можно найти в некоторых из приводимых решений. По формуле (1) (или в лоб) находим, что для такого многогранника d = 1004.
Ясно, что с ростом v уменьшаемое в (1) будет расти, а вычитаемое уменьшаться. Следовательно будет расти и d.
Картина, возникающая при уменьшении v, не столь очевидна. Ведь в этом случае в (1) будут уменьшаться и уменьшаемое и вычитаемое.
Так, при v = 1009, f = 1010 существует многогранник, имеющий одну 1007-угольную и 1009 треугольных граней. Впрочем, для того, чтобы понять, что у него больше диагоналей, чем вышеописанный, даже не нужно прибегать к формуле (1). Ведь, чтобы получить новый многогранник из предыдущего, достаточно малым шевелением:
а) перегнуть четырехугольные грани по диагонали (при этом добавятся две грани, два ребра и две диагонали);
б) спрямить одну из сторон 1008-угольного основания (при этом уйдут одна вершина, одна грань, два ребра и одна диагональ).
Итого, у нового многогранника получится 1004+2-1 = 1005 диагоналей.
Но уже следующее уменьшение v на 1 приведет к лавинообразному росту d. В самом деле, пусть v = 1008, f = 1011. Тогда наибольшее возможное значение h1 равно 1004 (иначе просто некуда будет «впихнуть» необходимое количество граней и ребер). Остальные 1010 грани - треугольники ((см. соответствующий граф на рисунке). Для такого многогранника формула (1) дает d=3009.
При дальнейшем уменьшении v наибольшее возможное h1 убывает более быстрыми темпами и, следовательно, d растет. Так, при наименьшем возможном v, равном 675, наибольшее h1 будет 5, а d=675·674/2-2017-5 = 225453.
Обсуждение
Подзаголовок «От двух до пяти», смутивший одних и вдохновивших других марафонцев, случайно достался этой задаче в наследство от ММ208.
Судя по присланным решениям, ММ218 оказалась достаточно сложной. Я же рассматривал ее, как весьма простую. По-видимому, это следствие того, что данную задачу я поставил уже после того, как исследовал вопросы о количестве диагоналей многогранников с фиксированным количеством вершин (граней). В частности, к этому времени я уже знал (и умел доказывать), что для минимизации количества диагоналей надо максимизировать число сторон самой большой грани.
Чтобы понять, насколько по-разному воспринимали сложность задачи участники и ведущий достаточно сравнить авторское решение с решением Владислава Франка, в котором Влад долго и скрупулезно обосновывает… неверный ответ ![]() Сразу отмечу (а то, ведь, не каждый осилит несколько страниц), что в решении Влада есть и верный ответ, но Влад предпочел сохранить в итоговом варианте весь тернистый путь к нему.
Сразу отмечу (а то, ведь, не каждый осилит несколько страниц), что в решении Влада есть и верный ответ, но Влад предпочел сохранить в итоговом варианте весь тернистый путь к нему.
Изначально я планировал давать 5 баллов за решения, в которых будут указаны многогранники с 1004 и 1055 диагоналями и приведены (возможно, не идеально строгие, но убедительные) соображения, подтверждающие невозможность меньшего числа диагоналей. Т. е. близкие к тому, что приведено мной. Но в процессе изучения решений участников, я слегка персмотрел эти критерии в сторону увеличения призовых баллов. Я старался не замечать откровения типа 553+553 = 1006 :) По крайней мере, при оценивании.
Разумеется, число 2017 не особенное по отношению к ММ218. Важна лишь его нечетность. Мне понравилось, что формула d=(e-9)/2 возвращает наименьшее возможное количество диагоналей многогранника с нечетным числом ребер для всех без исключения допустимых значений e и дает заведомо бессмысленные значения для тех e, для которых не существует многогранников. Многие другие формулы, связанные с количеством диагоналей многогранников, допускают исключения для малых значений параметров.
Награды
За решение ММ218 участникам начислены следующие призовые баллы:
Владислав Франк, Олег Полубасов и Анатолий Казмерчук - по 8;
Владимир Чубанов - 6;
Виктор Филимоненков и Владимир Дорофеев - по 4.
Эстетическая оценка задачи - 4.2 балла
ММ217
Конкурсная задача ММ217 (6 баллов)
Диагонали AC1 и BD1 шестигранника ABCDA1B1C1D1, все грани которого четырехугольны, пересекаются в точке O. Могут ли остальные пары диагоналей скрещиваться?
ММ216
Конкурсная задача ММ216 (10 баллов)
Назовем натуральное число n красивым, если наименьшее натуральное число, имеющее ровно n натуральных делителей, кратно n.
1. Доказать, что все праймориалы красивы.
2. Верно ли, что все факториалы красивы?
3. Сколько существует красивых чисел вида k7, где k - некоторое натуральное число?
4. Сколько существует красивых чисел вида 7kk, где k - некоторое натуральное число?
ММ215
Конкурсная задача ММ215 (4 балла)
На какое наименьшее количество тетраэдров можно разрезать шестиугольную призму?
ММ214
Конкурсная задача ММ214 (4 балла)
1. Все грани многогранника - n-угольники. При каких n это возможно?
2. При каком наименьшем числе граней существует многогранник, все грани которого пятиугольны?
ММ213
Конкурсная задача ММ213 (4 балла)
1. Пусть H = {h1, h_2,…, hf} , где f - количество граней, а hi - число сторон i -й грани. Какое наименьшее значение может принимать f-|H| ?
2. Пусть gi означает число i-угольных граней многогранника для каждого значения i . Могут ли все gi не превышать 2?
ММ212
Конкурсная задача ММ212 (4 балла)
Доказать, что любой многогранник, имеющий 2016 вершин, может быть разрезан на 4030 тетраэдров.
Решение
ММ211
Конкурсная задача ММ211 (3 балла)
Доказать, что при любом четном f > 4 существует многогранник, имеющий f граней, все грани которого четырехугольники.