| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Математический марафон
Продолжается 23-й конкурс в рамках Математического марафона
Какой-то единой тематикой задачи 23-го конкурса не объединены. Однако, легко разбить конкурсные задачи на три группы. Две из них посвящены традиционно любимым ведущим арифметике и комбинаторной геометрии. Третью можно условно озаглавить «Сон абитуриента в ночь перед ЕГЭ». Окажется ли этот сон кошмарным, скоро узнаем.
Выполняя взятые на себя обязательства, я постарался сделать задачи не слишком трудными. Впрочем, это замечание не касается последней задачи (оценка трудности которой - сама по себе трудная задача).
Еще одна цель, которую я преследовал, составляя задачи - избавиться от чрезмерного перекоса в сторону компьютерщины. Впрочем, от самого компьютера участникам избавляться не стоит, кое-где он пригодится.
Более ранний, по сравнению с предыдущими, старт конкурса не окажет существенного влияния на его дальнейший календарь. Как обычно, активная фаза конкурса начнется осенью. Это не значит, что нельзя решать задачи и присылать решения уже сейчас.Стать участником марафона может любой желающий. Некоторые задачи вполне доступны школьникам. Для решения других требуются знания, выходящие за рамки школьного курса. Одни задачи могут показаться вам интересными, а другие - не очень. На вкус и на цвет…
Но если любите поломать голову над нестандартными задачами, участвуйте, не стесняйтесь.
Жду от вас комментариев марафонских задач, а также пожеланий Марафону. Эта обратная связь позволит сделать Марафон интереснее для вас.
Не забывайте, пожалуйста, присылать вместе с Вашими решениями свои эстетические оценки задач по пятибалльной шкале.
Ведущий Марафона — Vladimir letsko
Текущие задачи
ММ226
Конкурсная задача ММ226 (5 баллов) Решения принимаются до 13.10.2017
Назовем натуральное число n счастливым, если оно является точной седьмой степенью, а седьмой (при упорядочении по возрастанию) натуральный делитель n равен количеству натуральных делителей n. А есть ли, вообще, счастье в жизни? В смысле, существуют ли счастливые числа?
ММ227
Конкурсная задача ММ227 (7 баллов) Решения принимаются до 20.10.2017
Пусть 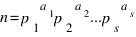 - каноническое разложение n. Обозначим через sopf(n) число
- каноническое разложение n. Обозначим через sopf(n) число 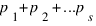 .
.
Назовем натуральное число k слабым, если уравнение x = k·sopf(x) неразрешимо в натуральных числах, и сильным в противном случае.
Доказать, что сильных чисел бесконечно много.
Найти наименьшее слабое число.
Доказать, что слабых чисел бесконечно много.
Терминология ММ228-230
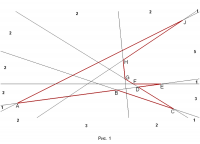
Несколько (не менее трех) прямых на плоскости называются прямыми общего положения, если любые 3 их них высекают треугольник. На рисунке 1 представлены 7 прямых общего положения.
Внешним контуром конфигурации n прямых общего положения назовем многоугольник, высекаемый данными прямыми. На рисунке 1 это красный девятиугольник ABCDEFGHJ.
Внешним циклом конфигурации назовем список количеств вершин внешних областей конфигурации, перечисленных в порядке обхода этих областей (направление и начало обхода не важны). Внешний цикл конфигурации, представленной на рисунке 1: (1, 2, 3, 3, 1, 3, 1, 5, 1, 2, 2, 2, 2, 2).
Выпуклыми вершинами внешнего контура назовем вершины, в которых углы меньше развернутого. На рисунке 1 выпуклыми вершинами являются A, C, E, J.
Обратными вершинами назовем вершины внешнего контура, углы при которых больше развернутого. На рисунке 1 это вершины B, D, F, G, H.
Элементарными отрезками назовем отрезки, концы которых являются соседним точками пересечения одной из прямых конфигурации с другими прямыми. Отрезок CD на рисунке 1 элементарен, а отрезок BC – нет.
Элементарными многоугольниками назовем многоугольники, стороны которых являются элементарными отрезками (одна сторона – один отрезок). Например, треугольник DEF на рисунке 1 элементарен, а треугольник BCD – нет.
Впадиной назовем участок внешнего контура между двумя соседними выпуклыми вершинами, содержащий хотя бы одну обратную вершину. Конфигурация, изображенная на рисунке 1 имеет 3 впадины ABC, CDE и EFGHJ.
Вектором граней конфигурации назовем упорядоченный набор из n-2 чисел (где n – количество прямых), первое из которых равно количеству элементарных треугольников, второе – количеству элементарных четырехугольников и т. д. Вектор граней конфигурации, представленной на рисунке 1 – [6, 8, 1, 0, 0].
ММ228
Конкурсная задача ММ228 (4 балла) Решения принимаются до 27.10.2017
Какое наименьшее число элементарных четырехугольников может быть в конфигурации из семи прямых общего положения?
ММ229
Конкурсная задача ММ229 (7 баллов) Решения принимаются до 03.11.2017
Петя нарисовал на доске несколько прямых общего положения так, что все попарные точки пересечения прямых попали на чертеж.
Вася выписал себе в тетрадь внешний цикл возникшей конфигурации: (1, 4, 3, 1, 4, 1, 2, 2, 3, 2, 3, 1, 2, 3, 1, 2, 4, 2, 1, 3).
После этого Петя стер рисунок. Сможет ли Вася восстановить:
1) количество прямых;
2) количество элементарных многоугольников:
3) количество выпуклых вершин;
4) количество элементарных отрезков, ограничивающих внешний контур;
5) количество сторон выпуклой оболочки внешнего контура;
6) суммарное число сторон элементарных многоугольников;
7) количество обратных вершин;
8) количество впадин;
9) количество сторон внешнего контура?
Примечание: Вася – умный.
ММ230
Конкурсная задача ММ230 (15 баллов) Решения принимаются до 01.12.2017
Может ли вектор граней конфигурации нескольких прямых общего положения начинаться с чисел 157, 5250, 52?
Разбор задач
ММ225
Конкурсная задача ММ225 (6 баллов)
Найти все значения параметра a, при которых уравнение (2a+3)x2 + xa + 3a - 1 = 0 имеет два целых корня.
Решение
Участники порадовали разнообразием подходов. Поэтому вновь приведу все решения: Евгения Гужавина, Владимира Дорофеева, Анатолия Казмерчука, Валентины Колыбасовой, Олега Полубасова, Виктора Филимоненкова, Владислава Франка. Решение Дмитрия Курашкина можно посмотреть здесь.
Обсуждение
Участники окончательно преодолели отпускную расслабленность и вновь не допустили ошибок в решении. Так держать!
В отличие использованных подходов (и предыдущей задачи), ответы не отличались разнообразием.
Окончательная оценка Евгения Гужавина сложилась с учетом добавки за несколько решений и сбавки за использование он-лайн солвера при решении простых диофантовых уравнений.
Награды
За решение задачи ММ224 участники Марафона получают следующие призовые баллы:
Анатолий Казмерчук - по 7;
Виктор Филимоненков, Владислав Франк, Олег Полубасов, Валентина Колыбасова, Владимир Дорофеев, Дмитрий Курашкин и Евгений Гужавин - по 6.
Эстетическая оценка задачи - 4.6 балла
ММ224
Конкурсная задача ММ224 (6 баллов)
В задаче, которую задали на дом Пете и Васе, требовалось найти площади треугольников, на которые разбивается исходный треугольник ABC трисектрисами, проведенными из вершины C. При сверке ответов у Пети и Васи совпали значения двух площадей: 2 и 4. Третья площадь у Пети оказалась равной 10, а у Васи - 20. Найти угол С, если известно, что один из учеников получил за домашнее задание пятерку.
Решение
Не смог выбрать лучшие решения. Поэтому приведу все: Евгения Гужавина; Владимира Дорофеева; Анатолия Казмерчука; Валентины Колыбасовой; Олега Полубасова; Виктора Филимоненкова; Владислава Франка.
Обсуждение
На этот раз все откликнувшиеся марафонцы - молодцы! Не допустили ошибок в решении. Поэтому, во избежание нарушения закона сохранения (и приумножения) ошибок во Вселенной, кое-что напутал ведущий.
Все было примерно как в старом (времен Norton Commander для DOS) анекдоте: Смотрю слева диск C и справа диск C. А зачем мне два одинаковых диска С? Взял и один отформатировал.
Когда я составлял задачку, в условии фигурировали буквенные обозначения исходного треугольника и трисектрис, из коих однозначно следовало, что именно средний треугольник имеет площадь 4 (догадка Валентиы Колыбасовой верна). Но в последний момент перед публикацией я (а зачем мне два одинаковых диска C?) решил убрать буковки. Буковки исчезли, а количество решений утроилось.
Присланные решения - настоящий разгул тригонометрии: равные ответы выглядят совершенно различными за счет разного представления.
И лишь Олег Полубасов упомянул возможность решения через окружности Аполлония. Сам я решал именно через них.
Награды
За решение задачи ММ224 участники Марафона получают следующие призовые баллы:
Олег Полубасов - 8;
Владислав Франк и Анатолий Казмерчук - по 7;
Виктор Филимоненков, Валентина Колыбасова, Владимир Дорофеев и Евгений Гужавин - по 6.
Эстетическая оценка задачи - 4.4 балла
ММ223
Конкурсная задача ММ223 (6 баллов)
Рассмотрим две задачки.
1. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
2. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую попавшуюся из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
Какое из условий выгоднее для жуликоватого Васи?
Примечание: Был ли журнал электронным – не важно. Но важно, что колы не ставим: разрешается использовать только оценки 2, 3, 4, 5
ММ222
Конкурсная задача ММ222 (6 баллов)
На доске написано 10 попарно различных натуральных чисел. После того как 5 из этих чисел разделили на 5, а другие 5 умножили на 5 возникли 10 попарно различных натуральных чисел, отличных от исходных. При этом сумма новых чисел оказалась в 3 раза больше суммы исходных. Пусть n - наименьшее возможное значение наибольшего из исходных чисел, для которых возможна описанная ситуация. Сколько существует различных наборов исходных чисел с наибольшим числом n+1?
ММ221
Конкурсная задача ММ221 (4 балла)
Сколько решений в натуральных числах имеет уравнение 3x4 + 2y3 = 37z ?
ММ220
Конкурсная задача ММ220 (15 баллов)
Найти наименьшее v такое, что существует многогранник, имеющий v вершин и 2016 диагоналей, а многогранника, имеющего v+1 вершину и 2016 диагоналей, не существует.