

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Содержание
Архив Марафона
ММ245
Конкурсная задача ММ245 (5 баллов)
В остроугольном треугольнике ABC провели высоту BH. Найти отношение площадей треугольников ABH и CBH, если первый из них подобен треугольнику из своих медиан, а второй – треугольнику из своих высот.
ММ244
Конкурсная задача ММ244 (6 баллов)
Галя предложила Ане, Боре и Васе такую загадку:
- Я задумала три попарно различных ненулевых цифры. Сейчас я по секрету сообщу Ане сумму квадратов, Боре произведение, а Варе сумму задуманных цифр. Попробуйте отгадать эти цифры.
Узнав сумму квадратов произведение и сумму, Аня, Боря и Вася сначала задумались, а затем разговорились:
А: Я не могу определить, что это за цифры.
Б: И я не могу.
В: И я тоже.
A: Тогда я их знаю!
Б: После этой реплики и я их знаю.
Что это за тройка цифр?
Примечание: У Ани, Бори и Васи все хорошо с арифметикой и логикой.
ММ243
Конкурсная задача ММ243 (5 баллов)⊥
В треугольнике ABC a<b<c и a⋅la=c⋅lc Найти угол β.
—
ММ242
Конкурсная задача ММ242 (5 баллов)
На сайте проводится опрос, кого из m номинированных футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует один раз за одного футболиста. На сайте отображается рейтинг каждого футболиста - доля голосов, отданных за него, в процентах, округленных до целого числа. После того, как проголосовали n посетителей, суммарный рейтинг номинантов составил 95%.
a) При каком наименьшем m такое возможно?
b) При каком наименьшем n такое возможно?
c) При каком наименьшем m+n такое возможно?
ММ241
Конкурсная задача ММ241 (4 балла)
При каких натуральных n множество {1, 2, …, n} можно разбить на два подмножества так, что произведение элементов первого подмножества равно сумме элементов второго?
ММ240
Конкурсная задача ММ2409 (13 баллов)
Проективную плоскость разбили несколькими прямыми общего положения. При этом образовалось ровно 17 треугольников. Сколько пятиугольников могло при этом получиться?
ММ239
Конкурсная задача ММ239 (10 баллов)
Решения принимаются до 17.11.2018
Существует ли выпуклый многогранник, у которого:
a) не менее половины граней - семиугольники;
b) более половины граней - семиугольники;
с) не менее половины граней - восьмиугольники;
d) более половины граней - восьмиугольники;
e) не менее половины граней - девятиугольники?
Примечание: Если у вас получается, что ответ на пункт «а» отрицательный, а на пункт «b» - положительный, подумайте еще.
ММ238
Конкурсная задача ММ238 (7 баллов)
Вася написал на доске k последовательных натуральных чисел и нашел их НОК - V.
Петя написал k последовательных натуральных чисел, больших Васиных, и тоже нашел их НОК - P.
Оказалось, что 2018 < V/P < 2019.
При каком наименьшем k такое возможно?
ММ237
Конкурсная задача ММ237 (7 баллов)
Студент математического факультета Вася Пупкин написал на доске некоторую перестановку A из S10 в виде произведения независимых циклов (запись каждого цикла начинается с наименьшего элемента; опускались ли в записи циклы длины 1 - неизвестно). Васины однокурсники прокомментировали эту запись.
Аня: A6 – тождественная перестановка.
Ваня: Длины всех циклов A – числа Фибоначчи.
Даня: В S10 существует ровно 3 перестановки, квадрат которых равен A.
Маня: Хм, уравнение X2 =B не может иметь в S10 ровно 3 решения ни при каком B.
Саня: Более того, количество решений уравнения X2 =B в S10 не может быть нечетным ни при каком B.
Таня: Квадрат наибольшего элемента в самом длинном цикле меньше порядка A.
Зина: A5 имеет столько же циклов, сколько и A.
Лина: Внутри всех циклов элементы строго возрастают.
Нина: Произведение всех элементов одного из циклов кратно произведению всех элементов более длинного цикла и сумме всех элементов более короткого.
Фаина: Зина, Лина и Нина правы.
Вася (умница и отличник) заметил, что количество верных утверждений его однокурсников равно наибольшей длине цикла в A.
Найдите A.
ММ236
Конкурсная задача ММ236 (7 баллов)
Натуральные числа от 1 до 4n разбили на четыре группы по n чисел в каждой. Оказалось, что произведение всех чисел из первой группы равно произведениям всех чисел из второй и третьей групп. Найти наименьшую возможную сумму чисел четвертой группы.
ММ235
Конкурсная задача ММ235 (7 баллов)
Существует ли выпуклый многогранник, у которого равны: количество ребер; количество диагоналей; суммарное количество диагоналей граней?
ММ234
Конкурсная задача ММ234 (5 баллов)
Функция g(n) натурального аргумента n задается так:
Пусть n натуральное число. Определим f(n) как число, полученное удалением последней цифры из десятичной записи n, увеличенное на квадрат этой цифры.
Например, f(576) = 57 + 36 = 93.
Тогда g(n) = |{n, f(n), f(f(n)), f(f(f(n))), …}|.
Пусть a и b – 2018-значные числа. Может ли оказаться, что g(a) = g(b) + 26?
ММ233
Конкурсная задача ММ233 (6 баллов)
Очередной отголосок ЕГЭ в Марафоне
При каких значениях параметра a множество точек плоскости, задаваемых системой
(x - a + 1)2 + (y - 3)2 ≤ 80,
(x - 3)2 + (y - 4a + 1)2 ≤ 20a2,
230 - 2a = |4x + 3y + 115 - a| + |4x + 3y - 115 + a|
является кругом?
ММ232
Конкурсная задача ММ232 (6 баллов)
Сколько решений в натуральных числах, имеет уравнение x3 + y3 = z3 - i для каждого i ∈ {1, 2, 4} ?
Я нашел воистину замечательные ответы на эти вопросы, но поля… Надеюсь, у конкурсантов с полями все хорошо.
ММ231
Конкурсная задача ММ231 (4 балла)
На сторонах AB, BC и AC египетского треугольника ABC выбрали точки C1, A1 и B1 соответственно. Оказалось, что треугольники AB1C1, BC1A1 и CA1B1 равновелики. Какую часть площади ABC составляет площадь треугольника A1B1C1 при условии, что последний - прямоугольный?
Терминология ММ228-230
Несколько (не менее трех) прямых на плоскости называются прямыми общего положения, если любые 3 их них высекают треугольник. На рисунке 1 представлены 7 прямых общего положения.
Внешним контуром конфигурации n прямых общего положения назовем многоугольник, высекаемый данными прямыми. На рисунке 1 это красный девятиугольник ABCDEFGHJ.
Внешним циклом конфигурации назовем список количеств вершин внешних областей конфигурации, перечисленных в порядке обхода этих областей (направление и начало обхода не важны). Внешний цикл конфигурации, представленной на рисунке 1: (1, 2, 3, 3, 1, 3, 1, 5, 1, 2, 2, 2, 2, 2).
Выпуклыми вершинами внешнего контура назовем вершины, в которых углы меньше развернутого. На рисунке 1 выпуклыми вершинами являются A, C, E, J.
Обратными вершинами назовем вершины внешнего контура, углы при которых больше развернутого. На рисунке 1 это вершины B, D, F, G, H.
Элементарными отрезками назовем отрезки, концы которых являются соседним точками пересечения одной из прямых конфигурации с другими прямыми. Отрезок CD на рисунке 1 элементарен, а отрезок BC – нет.
Элементарными многоугольниками назовем многоугольники, стороны которых являются элементарными отрезками (одна сторона – один отрезок). Например, треугольник DEF на рисунке 1 элементарен, а треугольник BCD – нет.
Впадиной назовем участок внешнего контура между двумя соседними выпуклыми вершинами, содержащий хотя бы одну обратную вершину. Конфигурация, изображенная на рисунке 1 имеет 3 впадины ABC, CDE и EFGHJ.
Вектором граней конфигурации назовем упорядоченный набор из n-2 чисел (где n – количество прямых), первое из которых равно количеству элементарных треугольников, второе – количеству элементарных четырехугольников и т. д. Вектор граней конфигурации, представленной на рисунке 1 – [6, 8, 1, 0, 0].
ММ230
Конкурсная зхадача ММ230 (15 баллов)
Может ли вектор граней конфигурации нескольких прямых общего положения начинаться с чисел 157, 5250, 52?
ММ229
Конкурсная задача ММ229 (7 баллов)
Петя нарисовал на доске несколько прямых общего положения так, что все попарные точки пересечения прямых попали на чертеж.
Вася выписал себе в тетрадь внешний цикл возникшей конфигурации: (1, 4, 3, 1, 4, 1, 2, 2, 3, 2, 3, 1, 2, 3, 1, 2, 4, 2, 1, 3).
После этого Петя стер рисунок. Сможет ли Вася восстановить:
1) количество прямых;
2) количество элементарных многоугольников:
3) количество выпуклых вершин;
4) количество элементарных отрезков, ограничивающих внешний контур;
5) количество сторон выпуклой оболочки внешнего контура;
6) суммарное число сторон элементарных многоугольников;
7) количество обратных вершин;
8) количество впадин;
9) количество сторон внешнего контура?
Примечание: Вася – умный.
ММ228
Конкурсная задача ММ228 (4 балла)
Какое наименьшее число элементарных четырехугольников может быть в конфигурации из семи прямых общего положения?
ММ227
Конкурсная зхадача ММ227 (7 баллов)
Пусть 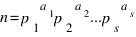 - каноническое разложение n. Обозначим через sopf(n) число
- каноническое разложение n. Обозначим через sopf(n) число 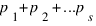 .
.
Назовем натуральное число k слабым, если уравнение x = k*sopf(x) неразрешимо в натуральных числах, и сильным в противном случае.
Доказать, что сильных чисел бесконечно много.
Найти наименьшее слабое число.
Доказать, что слабых чисел бесконечно много.
ММ226
Конкурсная зхадача ММ226 (5 баллов)
Назовем натуральное число n счастливым, если оно является точной седьмой степенью, а седьмой (при упорядочении по возрастанию) натуральный делитель n равен количеству натуральных делителей n. А есть ли, вообще, счастье в жизни? В смысле, существуют ли счастливые числа?
ММ225
Конкурсная задача ММ225 (6 баллов)
Найти все значения параметра a, при которых уравнение (2a+3)x2 + xa + 3a - 1 = 0 имеет два целых корня.
ММ224
Конкурсная задача ММ224 (6 баллов)
В задаче, которую задали на дом Пете и Васе, требовалось найти площади треугольников, на которые разбивается исходный треугольник ABC трисектрисами, проведенными из вершины C. При сверке ответов у Пети и Васи совпали значения двух площадей: 2 и 4. Третья площадь у Пети оказалась равной 10, а у Васи - 20. Найти угол С, если известно, что один из учеников получил за домашнее задание пятерку.
ММ223
Конкурсная задача ММ223 (6 баллов)
Рассмотрим две задачки.
1. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
2. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую попавшуюся из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
Какое из условий выгоднее для жуликоватого Васи?
Примечание: Был ли журнал электронным – не важно. Но важно, что колы не ставим: разрешается использовать только оценки 2, 3, 4, 5
ММ222
Конкурсная задача ММ222 (6 баллов)
На доске написано 10 попарно различных натуральных чисел. После того как 5 из этих чисел разделили на 5, а другие 5 умножили на 5 возникли 10 попарно различных натуральных чисел, отличных от исходных. При этом сумма новых чисел оказалась в 3 раза больше суммы исходных. Пусть n - наименьшее возможное значение наибольшего из исходных чисел, для которых возможна описанная ситуация. Сколько существует различных наборов исходных чисел с наибольшим числом n+1?
ММ221
Конкурсная задача ММ221 (4 балла)
Сколько решений в натуральных числах имеет уравнение 3x4 + 2y3 = 37z ?
ММ220
Конкурсная задача ММ220 (15 баллов)
Найти наименьшее v такое, что существует многогранник, имеющий v вершин и 2016 диагоналей, а многогранника, имеющего v+1 вершину и 2016 диагоналей, не существует.
ММ219
Конкурсная задача ММ219 (8 баллов)
Какое наибольшее количество диагоналей может иметь одиннадцатигранник?
ММ218
Конкурсная задача ММ218 (5 баллов)
Найти наименьшее возможное количество диагоналей многогранника, имеющего 2017 ребер.
ММ217
Конкурсная задача ММ217 (6 баллов)
Диагонали AC1 и BD1 шестигранника ABCDA1B1C1D1, все грани которого четырехугольны, пересекаются в точке O. Могут ли остальные пары диагоналей скрещиваться?
ММ216
Конкурсная задача ММ216 (10 баллов)
Назовем натуральное число n красивым, если наименьшее натуральное число, имеющее ровно n натуральных делителей, кратно n.
1. Доказать, что все праймориалы красивы.
2. Верно ли, что все факториалы красивы?
3. Сколько существует красивых чисел вида k7, где k - некоторое натуральное число?
4. Сколько существует красивых чисел вида 7k, где k - некоторое натуральное число?
ММ215
Конкурсная задача ММ215 (4 балла)
На какое наименьшее количество тетраэдров можно разрезать шестиугольную призму?
ММ214
Конкурсная задача ММ214 (4 балла)
1. Все грани многогранника - n-угольники. При каких n это возможно?
2. При каком наименьшем числе граней существует многогранник, все грани которого пятиугольны?
ММ213
Конкурсная задача ММ213 (4 балла)
1. Пусть H = {h1, h_2,…, hf} , где f - количество граней, а hi - число сторон i -й грани. Какое наименьшее значение может принимать f-|H| ?
2. Пусть gi означает число i-угольных граней многогранника для каждого значения i . Могут ли все gi не превышать 2?
ММ212
Конкурсная задача ММ212 (4 балла)
Доказать, что любой многогранник, имеющий 2016 вершин, может быть разрезан на 4030 тетраэдров.
Решение
ММ211
Конкурсная задача ММ211 (3 балла)
Доказать, что при любом четном f > 4 существует многогранник, имеющий f граней, все грани которого четырехугольники.
ММ210
Конкурсная задача ММ210 (13 баллов)
1. Пусть М = {ha, hb, hc, ba, bb, bc, ma, mb, mc} - множество, состоящее из величин высот, биссектрис, и медиан некоторого треугольника. Сколько элементов может быть в M?
2. Пусть в разностороннем треугольнике ABC (a < b < c) и множество М из п.1 содержит 9 элементов. Соответствующие числа расположили в порядке возрастания. Сколько различных упорядочиваний может при этом получится?
3. Тот же вопрос для случая, когда среди чисел {ha, hb, hc, ba, bb, bc, ma, mb, mc} могут быть одинаковые. (В этом случае полагаем a ≤ b ≤ c и рассматриваем строгое упорядочивание классов одинаковых величин. Перестановки внутри класса не важны.)
Примечание.
Получить ответ для каждого из случаев:
1) рассматриваются только невырожденные треугольники;
2) допускаются вырожденные треугольники (все вершины лежат на одной прямой).
ММ209
Конкурсная задача ММ209 (9 баллов)
Эта задача прямое продолжение задач ММ29 и ММ39
Назовем натуральное число a третькубом, по основанию g, если дважды приписав в g-ичной системе a к себе получим полный куб. Доказать, что существует бесконечно много оснований g, для которых есть третькубы.
ММ208
Конкурсная задача ММ208 (7 баллов)
От двух до пяти.
Найти наименьшее натуральное число, представимое в виде суммы пяти натуральных слагаемых не менее чем четырьмя способами, таким образом, что любые три слагаемых взаимно просты, а любые два не взаимно просты,.
ММ207
Конкурсная задача ММ207 (13 баллов)
Задача ММ207 является прямым продолжением задач ММ77 и ММ206
Обозначим через A(a,d) максимально возможное количество последовательных натуральных чисел таких, что первое из имеет ровно a натуральных делителей, второе - a+d, третье - a+2d и т.д. (иными словами, количества делителей последовательных чисел образуют арифметическую прогрессию с первым членом a и разностью d).
1) найти наибольшее возможное значение A(n,1);
2) найти наибольшее возможное значение A(n,3);
3) найти A(2,2);
4) найти A(4,2);
5) доказать, что при подходящем n A(n,2) ≥ 8.
ММ206
Конкурсная задача ММ206 (11 баллов)
Задача ММ206 является прямым продолжением задачи ММ77
Каждое из n натуральных чисел, идущих подряд, имеет ровно k натуральных делителей. Какое наибольшее значение может принимать n, если
1) k = 18;
2) k = 20;
3) k = 22;
4) k = 202.
Замечание: Относительно скромное количество призовых баллов за эту задачу обусловлено тем, что при ее решении можно воспользоваться не только решением ММ77, но и результатами статьи, на которую есть ссылка в обсуждении.
ММ205
Конкурсная задача ММ205 (7 баллов)
Вася выписывает в порядке возрастания натуральные числа, имеющие по 2016 натуральных делителей. На каком шаге он впервые выпишет число, не кратное 2016?
ММ204
Конкурсная задача ММ204 (5 баллов)
Найти натуральное число, которое в трех различных системах счисления записывается 102, 201 и 20001 соответственно.
ММ203
Конкурсная задача ММ203 (5 баллов)
Единичный квадрат разрезали на 5 равновеликих фигур отрезками, параллельными диагоналям. Найти наименьшую возможную суммарную длину этих отрезков.
ММ202
Конкурсная задача ММ202 (5 баллов)
При каких значениях параметра a разрешимо уравнение x2 - a = [x]{x}?
ММ201
Конкурсная задача ММ201 (3 балла)
Для каждого натурального k найти все возможные n, при которых множество {1, 2, …, n} можно разбить на классы так, что наибольший элемент в каждом классе ровно в k раз больше количества элементов класса.
