

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ15
Конкурсная задача ММ15 (9 баллов)
В качестве вводной предлагается задачка из конкурса 'Кенгуру' 1998 года:
Мама печет 6 пирогов: сначала пирог с абрикосами (А), потом с брусникой (Б), с вишней (В), с грибами (Г), с джемом (Д) и с ежевикой (Е). Пока она этим занимается, на кухню иногда забегают дети и каждый раз съедают самый горячий пирог. В каком порядке не могли быть съедены пироги?
1) АБВГДЕ; 2) АБДГВЕ; 3) ВБДГЕА; 4) ГДЕБВА; 5) ЕДГВБА. (1 балл)
А теперь основная часть задачи:
Назовем перестановку множества {1,2,…,n} возможной, если она удовлетворяет условию вводной задачки. Сколько возможных перестановок для n=20? (8 баллов)
Решение
Ответ на первый вопрос задачи очевиден: невозможна последовательность ГДЕБВА. После съедения пирога Е, согласно условию, должен был быть съеден пирог В.
Рассмотрим основную часть задачи.
Для тех, кто знаком с числами Каталана (и сумеет разглядеть их в условии), задача ММ15 является достаточно легкой. В самом деле, по условию задачи чем позднее приготовлен каждый из n пирогов (скобка открылась), тем раньше он съеден (скобка закрылась), что соответствует правильной расстановке n пар скобок. Таким образом, количество возможных перестановок на множестве {1,2,…n} равно количеству правильных расстановок n пар скобок, которое, в свою очередь есть n-ое число Каталана.
Приведу более громоздкое, но зато явное (в лоб) решение 15-й задачи:
Рассмотрим количество возможных перестановок для небольших значений n. При этом отдельно посчитаем перестановки, начинающиеся с 1, 2, … n. Результаты занесем в таблицу.
| n\i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 1 | 1 | ||||
| 3 | 2 | 2 | 1 | |||
| 4 | 5 | 5 | 3 | 1 | ||
| 5 | 14 | 14 | 9 | 4 | 1 | |
| 6 | 42 | 42 | 28 | 14 | 5 | 1 |
Обозначим через A(n,i) количество возможных перестановок множества {1,2,..,n}, начинающихся с i. Из таблицы легко просматривается рекуррентная формула
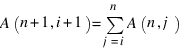 .
.
Для того, чтобы убедиться в справедливости этой формулы, заметим, что между возможными перестановками n-элементного множества, начинающимися с элемента не меньшего i, и возможными перестановками n+1-элементного множества, начинающимися в точности с элемента i+1 существует биекция. Эта биекция строится так: к перестановке n-элементного множества приписывается слева элемент i+1, а остальные элементы переписываются, причем элементы большие i увеличиваются на 1. Продолжив приведенную выше таблицу до 20-й строки и просуммировав элементы этой строки (разумеется, эти действия совсем не обязательно производить вручную), получим ответ - 6564120420 (двадцатое число Каталана).
Обсуждение
Для чисел Каталана Cn можно получить целых ряд явных и рекуррентных соотношений:
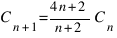 ;
;
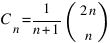 ;
;
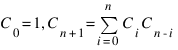 .
.
Награды
За правильное решение этой задачи Борис Бух получает 9 призовых баллов.