

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ198
Конкурсная задача ММ198 (8 баллов)
Будем говорить, что n-угольник относится к классу s, если его можно триангулировать на n-2 треугольника внутренними диагоналями в точности s различными способами. Найти три наименьших и три наибольших значения s для n = 20.
Решение
Привожу решения Виктора Филимоненкова, Олега Полубасова и Анатолия Казмерчука.
Обсуждение
На ММ198 получено наименьшее в 20-м туре количество решений. По-видимому, это свидетельствует о трудности задачи (первоначальная цена задачи - показатель весьма субъективный). Альтернативное объяснение - задача не вызвала интереса участников - не проходит, ввиду максимально возможной эстетической оценки задачи. Хотя… процитирую комментарий Дмитрия Пашуткина «Мне показалось, что эта задача из тех, интерес к которым растет прямо пропорционально времени, затраченному на их решение, из разряда «аппетит приходит во время еды» :) Условие на первый взгляд создает впечатление громоздкости требуемых для решения построений, но стоит только взяться и дальше уже оторваться невозможно.»
Отмечу два разных подхода, примененных участниками к конструированию нужных многоугольников: «склеивание» многоугольников с меньшим числом сторон по общей стороне; «вдавливание» некоторых вершин выпуклого многоугольника. Для получения максимальных значений s конкурсанты естественно использовали второй подход. Для малых значений s большинство конкурсантов использовали первый подход и «уперлись» в случай s=11. В то время как «вдавливание» (см. решение Олега Полубасова) позволяет легко преодолеть этот барьер.
В некоторых решениях (например, у Анатолия Казмерчука) приведены (достаточно легко находимые) полные списки возможных значений s для n < 6. Усилю этот результат, списком для n = 7:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 18, 19, 23, 28, 42}.
Разумеется, можно продвинуться и дальше. Но задача описания всех возможных значений s (или хотя бы их количества) для произвольного «n», мягко говоря, очень трудна.
Рост n приводит некому «фрактально-комбинаторному взрыву». «Фрактально» - потому что в формулах для подсчета плодятся самоподобные подформулы. А «взрыву» - потому что плодятся они весьма активно.
Затруднено даже продвижение в изучении максимально возможных значений s. Это затруднение вызвано тем, что с ростом n, значения s, полученные однотипным формулам могут меняться местами (иногда совпадая).
Этот момент описан в решении Анатолия Казмерчука: Действительно, подставляя разные n в формулы Cn-2-Cn-3-2Cn-4 и Cn-2-2Cn-3+Cn-4 (соответствующие возможным классам n-угольников) получим:
для n=7 18 и 19 соответственно;
для n=8 оба раза по 62;
для n=9 213 и 207.
Очередной раз я испытывал определенные затруднения при распределении призовых баллов. Предвосхищая чаяния ведущего, многие участники не ограничились шестью требуемыми значениями s. Понятно, что их усилия должны быть поощрены дополнительными баллами. В значительно меньшей степени понятно что лучше: продвинуться в нахождении больших значений дальше конкурентов, но при этом пропустить некоторые значения в «гарантированном» списке, или ограничиться меньшим количеством значений s, не доходя до пропущенного значения. Итоги моих сомнений см. в разделе «Награды».
А здесь приведу первый (если я тоже чего-то не пропустил) пропущенный случай в «гарантированном» списке Олега.
У 20-угольника на рисунке 1 отсутствуют внешние диагонали A17A20 и A18A20. Поэтому он относится к классу C18-C17-C16=312636240
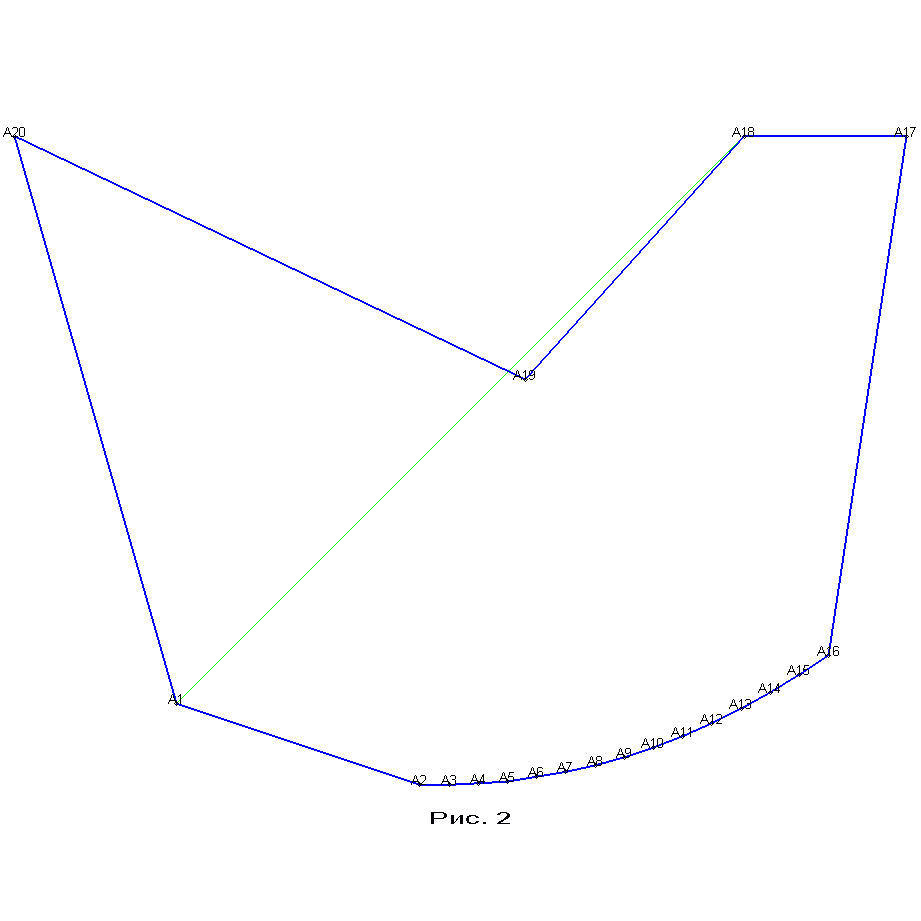
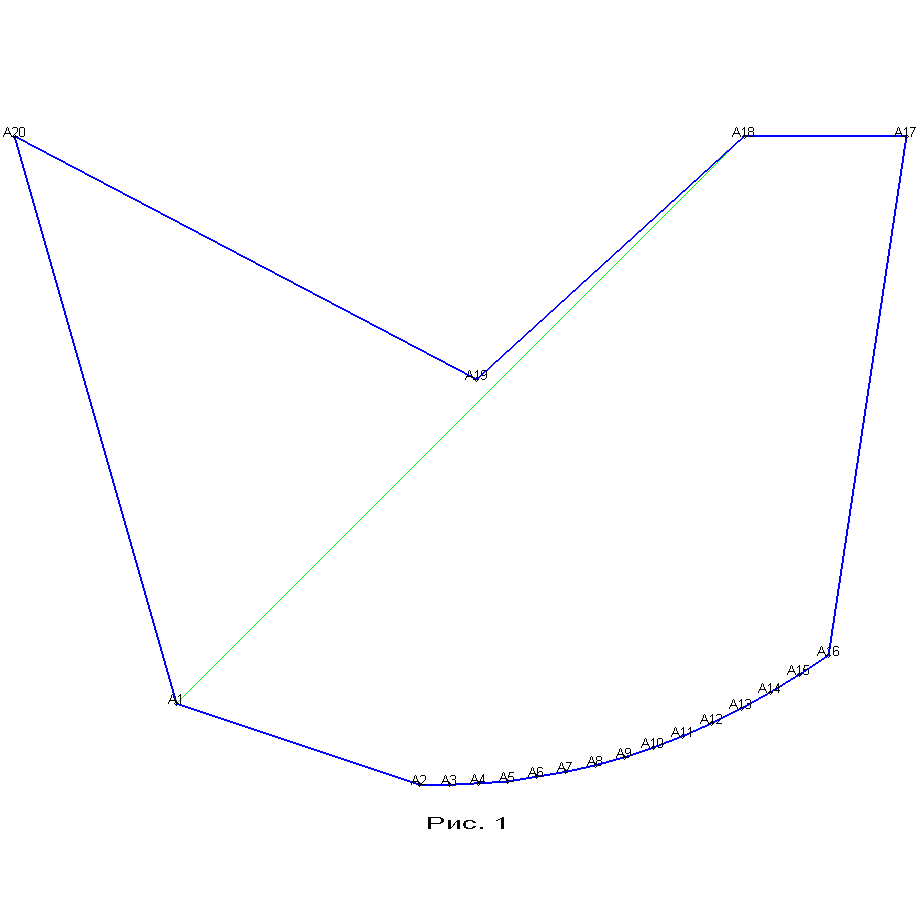 Если же немного сместить вправо вершину A19 (рис. 2), то исчезнут триангуляции, содержащие диагональ A1A18. Это в точности триангуляции выпуклого 18-угольника A1A2…A18. Поэтому у 20-угольника на рисунке 2 в точности C18-C17-2C16=277278570 триангуляций.
Если же немного сместить вправо вершину A19 (рис. 2), то исчезнут триангуляции, содержащие диагональ A1A18. Это в точности триангуляции выпуклого 18-угольника A1A2…A18. Поэтому у 20-угольника на рисунке 2 в точности C18-C17-2C16=277278570 триангуляций.
Награды
За решение задачи ММ198 участникам начислены следующие призовые баллы: Олег Полубасов и Анатолий Казмерчук - по 11; Сергей Половинкин - 10; Виктор Филимоненков и Дмитрий Пашуткин - по 8; Ариадна - 6.
Эстетическая оценка задачи - 5 баллов