| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ218
Конкурсная задача ММ218 (5 баллов)
Найти наименьшее возможное количество диагоналей многогранника, имеющего 2017 ребер.
Решение
Привожу решения Владимира Чубанова, Олега Полубасова, Анатолия Казмерчука и Владислава Франка.
Решение Владимира Чубанова
ММ218
Найти наименьшее возможное количество диагоналей многогранника, имеющего 2017 ребер.
Ответ: 1004 диагоналей.
![[img]http://s019.radikal.ru/i600/1611/e3/e8f7633cbe66.png[/img]|рис. 1 [img]http://s019.radikal.ru/i600/1611/e3/e8f7633cbe66.png[/img]|рис. 1](/lib/exe/fetch.php?w=200&tok=5021ba&media=marathon:pic_mm218.png) Пример на 1004 построить легко (см. рисунок). Поставили треугольную призму «домиком» и с одной стороны – со стороны AB – добавили 1004 точки в плоскости ABDF (на рисунке отмечена только часть этих точек). Получили 1008 точек основания и 2 точки «сверху».
Пример на 1004 построить легко (см. рисунок). Поставили треугольную призму «домиком» и с одной стороны – со стороны AB – добавили 1004 точки в плоскости ABDF (на рисунке отмечена только часть этих точек). Получили 1008 точек основания и 2 точки «сверху».
Количество рёбер: 1008+1004+4+1 = 2017;
Количество (пространственных) диагоналей: 1004 – все новые точки соединены с т.E. Других диагоналей нет.
Аргументы в пользу того, что меньше быть не может.
При рассмотрении суммарно всех диагоналей (пространственные + диагонали граней) нетрудно заметить, что наиболее выгодная стратегия лежит не в уменьшении числа вершин и не в разделении вершин по разным граням, а в максимальной консолидации вершин в одной грани-плоскости (поскольку \binom{n}{2} растёт квадратично, при таком количестве точек это перевешивает остальные стратегии).
Поднять только одну вершину над плоскостью недостаточно – количество рёбер будет чётным.
Поднять 2 вершины над плоскостью можно несколькими принципиально разными способами, которые несложно перебрать руками и убедиться, что представленный вариант принадлежит множеству самых выгодных.
Кроме того, приведу и свое решение задачи.
Авторское решение
Я специально не стал заострять внимание на технических деталях, чтобы не скрыть в них основные (довольно простые) идеи.
Пусть многогранник имеет v вершин, e ребер и f граней, а h1,h2, …, f - количества сторон граней. Очевидно, что количество диагоналей такого многогранника многогранника вычисляется по формуле:
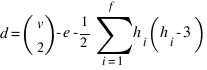 (1)
(1)
Легко видеть, что при фиксированных e и f сумма
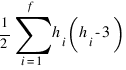
будет тем меньше, чем равномернее распределены значения hi. И, соответственно, тем больше, чем больше самое большое из hi (в дальнейшем будем считать, что это h1.
При четных e h1 может достигать e/2. Этот случай соответствует пирамидам, у которых d=0.
В нашем случае наибольшее значение h1 = 1008 достигается при v = 1010, f = 1009. Соответствующие многогранники (еще две его грани четырехугольны, а остальные треугольны) легко строится. Их изображения можно найти в некоторых из приводимых решений. По формуле (1) (или в лоб) находим, что для такого многогранника d = 1004.
Ясно, что с ростом v уменьшаемое в (1) будет расти, а вычитаемое уменьшаться. Следовательно будет расти и d.
Картина, возникающая при уменьшении v, не столь очевидна. Ведь в этом случае в (1) будут уменьшаться и уменьшаемое и вычитаемое.
Так, при v = 1009, f = 1010 существует многогранник, имеющий одну 1007-угольную и 1009 треугольных граней. Впрочем, для того, чтобы понять, что у него больше диагоналей, чем вышеописанный, даже не нужно прибегать к формуле (1). Ведь, чтобы получить новый многогранник из предыдущего, достаточно малым шевелением:
а) перегнуть четырехугольные грани по диагонали (при этом добавятся две грани, два ребра и две диагонали);
б) спрямить одну из сторон 1008-угольного основания (при этом уйдут одна вершина, одна грань, два ребра и одна диагональ).
Итого, у нового многогранника получится 1004+2-1 = 1005 диагоналей.
Но уже следующее уменьшение v на 1 приведет к лавинообразному росту d. В самом деле, пусть v = 1008, f = 1011. Тогда наибольшее возможное значение h1 равно 1004 (иначе просто некуда будет «впихнуть» необходимое количество граней и ребер). Остальные 1010 грани - треугольники ((см. соответствующий граф на рисунке). Для такого многогранника формула (1) дает d=3009.
При дальнейшем уменьшении v наибольшее возможное h1 убывает более быстрыми темпами и, следовательно, d растет. Так, при наименьшем возможном v, равном 675, наибольшее h1 будет 5, а d=675·674/2-2017-5 = 225453.
Обсуждение
Подзаголовок «От двух до пяти», смутивший одних и вдохновивших других марафонцев, случайно достался этой задаче в наследство от ММ208.
Судя по присланным решениям, ММ218 оказалась достаточно сложной. Я же рассматривал ее, как весьма простую. По-видимому, это следствие того, что данную задачу я поставил уже после того, как исследовал вопросы о количестве диагоналей многогранников с фиксированным количеством вершин (граней). В частности, к этому времени я уже знал (и умел доказывать), что для минимизации количества диагоналей надо максимизировать число сторон самой большой грани.
Чтобы понять, насколько по-разному воспринимали сложность задачи участники и ведущий достаточно сравнить авторское решение с решением Владислава Франка, в котором Влад долго и скрупулезно обосновывает… неверный ответ ![]() Сразу отмечу (а то, ведь, не каждый осилит несколько страниц), что в решении Влада есть и верный ответ, но Влад предпочел сохранить в итоговом варианте весь тернистый путь к нему.
Сразу отмечу (а то, ведь, не каждый осилит несколько страниц), что в решении Влада есть и верный ответ, но Влад предпочел сохранить в итоговом варианте весь тернистый путь к нему.
Изначально я планировал давать 5 баллов за решения, в которых будут указаны многогранники с 1004 и 1055 диагоналями и приведены (возможно, не идеально строгие, но убедительные) соображения, подтверждающие невозможность меньшего числа диагоналей. Т. е. близкие к тому, что приведено мной. Но в процессе изучения решений участников, я слегка персмотрел эти критерии в сторону увеличения призовых баллов. Я старался не замечать откровения типа 553+553 = 1006 :) По крайней мере, при оценивании.
Разумеется, число 2017 не особенное по отношению к ММ218. Важна лишь его нечетность. Мне понравилось, что формула d=(e-9)/2 возвращает наименьшее возможное количество диагоналей многогранника с нечетным числом ребер для всех без исключения допустимых значений e и дает заведомо бессмысленные значения для тех e, для которых не существует многогранников. Многие другие формулы, связанные с количеством диагоналей многогранников, допускают исключения для малых значений параметров.
Награды
За решение ММ218 участникам начислены следующие призовые баллы:
Владислав Франк, Олег Полубасов и Анатолий Казмерчук - по 8;
Владимир Чубанов - 6;
Виктор Филимоненков и Владимир Дорофеев - по 4.
Эстетическая оценка задачи - 4.2 балла