

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
174
Конкурсная задача ММ174 (А-4) (7 баллов)
Найти наименьшее натуральное число, произведение всех натуральных делителей которого заканчивается
а) ровно 2013 нулями;
б) не менее чем 2013 нулями.
Примечание:
Система счисления десятичная.
Решение
Приведу здесь лишь набросок решения. С более подробным вариантом можно ознакомиться здесь
Ясно, что в каноническом разложении искомых чисел должны присутствовать множители 2 и 5. Причем показатель степени у пятерки не больше, чем у двойки (иначе их можно было бы поменять местами и уменьшить число).
Потому искомые числа имеют вид a = 5sn, где n кратно 2s. Произведение всех делителей числа a будет заканчиваться τ(n)s(s+1)/2 нулями.
a) 2013 = 3*11*61. Это дает возможность пложить s = 3 (что выгоднее, чем s=1). Поэтому наименьшее число, произведение делителей которого заканчивается 2013-ю нулями это 26031052
б) Пусть 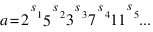 . Ясно, что s1 ≥ s2 и s3 ≥ s4 ≥ s5 ≥…
Кроме того, поскольку 211 > 2013, ясно, что количество различных простых сомножителей в разложении a не превосходит 12.
Учитывая, что произведение делителей числа 2115735 оканчивается 2016-ю нулями. приходим к выводу, что показатели простых делителей, больших 5 (если таковые имеются в искомом числе), должны быть меньше 5.
Не сложно находятся ограничения сверху и для показателей двойти, тройки и пятерки.
В результате искомое число получаемое после небольшого перебора - 25553271111131=900900000.
. Ясно, что s1 ≥ s2 и s3 ≥ s4 ≥ s5 ≥…
Кроме того, поскольку 211 > 2013, ясно, что количество различных простых сомножителей в разложении a не превосходит 12.
Учитывая, что произведение делителей числа 2115735 оканчивается 2016-ю нулями. приходим к выводу, что показатели простых делителей, больших 5 (если таковые имеются в искомом числе), должны быть меньше 5.
Не сложно находятся ограничения сверху и для показателей двойти, тройки и пятерки.
В результате искомое число получаемое после небольшого перебора - 25553271111131=900900000.
Обсуждение
Сергей Половинкин нашел в Интернете задачу (предлагаемую в качестве образца задачи С6 ЕГЭ), где требовалось найти намиеньше натуральное число, произведение делителей которого заканчивается на 399 нулей. Каюсь, одиннадцатиклассники, у которых я веду факультатив, приносили мне эту задачу (только не уверен, что там именно 399 нулей было). И именно она легла в основу ММ174. Единственное существенное изменение - добавление пункта б), на мой взгляд, гораздо более содержательного, чем а). В частности, у меня ушло на второй пункт раз в 10 больше времени, чем на первый.
Поясню, как я оценивал решения. Одного балла недосчитались те участники, которые (хотя и упомянули, что решали пункт б) перебором) не привели ограничений, делающих перебор конечным.
Если же такие ограничения (пусть и не оптимальные) в решении были приведены, я ставил оценку 7 баллов. Но только при условии, что ответ верен ![]()
Сергей Половинкин (неожиданно для меня) нашел в условии скрытый намек на исследование задачи для других систем счисления. И прислал мне набросок такого обобщения. Мне думается, что такое обобщение не вызывает особого интереса (в отличие, например, от ММ175). Поэтому дополнительных призовых баллов не было. Что-то в текущем туре я стал жаден на дополнительные баллы. Но обещаю исправиться.
Награды
За решение задачи ММ174 Виктор Филимоненков, Алексей Извалов, Анатолий Казмерчук и Алексей Волошин получают по 7 призовых баллов. Сергей Половинкин и Олег Полубасов получают по 6 призовых баллов. Евгений Гужавин - 5 призовых баллов, а Николай Дерюгин - 4 призовых балла.
Эстетическая оценка задачи - 4.4 балла