

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ21
Конкурсная задача ММ21 (10 баллов)
Доказать, что уравнение 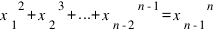 (1) имеет бесконечно много решений в натуральных числах:
(1) имеет бесконечно много решений в натуральных числах:
a) при любом нечетном простом n (4 балла);
б) при n=9 (6 баллов).
Решение
Как выяснилось, благодаря марафонцам, решившим эту задачу, подразделение ее на пункты а) и б) оказалось весьма искусственным.
При n=5 имеем решение: 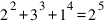
Это решение можно продолжить для любого n, большего 4:

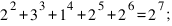
И т.д.
Для случая n=3, наличие решений очевидно.
Не сложно найти решение и для n=4: 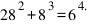 Но из наличия хотя бы одного решения сразу вытекает наличие бесконечного числа решений. Действительно, если
Но из наличия хотя бы одного решения сразу вытекает наличие бесконечного числа решений. Действительно, если 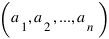 - решение, а s - НОК чисел 2, 3,.., n,
- решение, а s - НОК чисел 2, 3,.., n,
то при любом k 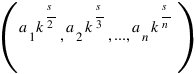 - тоже решение.
- тоже решение.
Таким образом, (1) имеет бесконечно много решений при любом n, большем 2.
Обсуждение
Объясню, откуда взялись пункты а) и б) в условии.
Составляя эту задачу, я отталкивался от такого рассуждения:
Пусть n простое число большее 3. Обозначим a = n-2, k = НОК(2, 3,.., n-1), kn = m.
В силу простоты n, n и k взаино просты. Поэтому среди чисел k+1, 2k+1,…, (n-1)k+1 найдется кратное n. Обозначим его s+1.
Тогда 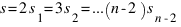 и
и 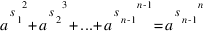
При составном n такое рассуждение уже не проходит. При n=9 можно сконструировать решение (1), оперируя степенями тройки и пользясь соотношением 
Похожую конструкцию можно соорудить и отталкиваясь от степеней двойки.
Получится совсем уж похоже на то, что предложено перечисленными ниже участниками марафона и приведено в разделе 'решение'.
Несмотря на это сходство, решения, проходящего для любого n, больше 4, я не заметил.
Несколько видоизмененный вариант этой задачи неожиданно для меня был опубликован в журнале «Квант» №1-2006 в разделе КМШ.
Награды
За правильное (более универсальное, чем авторское) решение этой задачи Владимир Трушков, Макс Алексеев и Борис Бух получают по 12 призовых баллов.