

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Содержание
ММ32
Конкурсная задача ММ32 (3 баллов)
Рассмотрим векторы, координаты которых в некотором ортонормированном базисе n-мерного пространства представляют собой перестановки множества {1, 2,.., n}. Каким может быть максимальный угол между такими векторами?
Решение
Ясно, что надо минимизировать косинус угла между векторами. Произведение модулей векторов постоянно и равно 1+4+…+n2. Минимум же скалярного произведения достигается, например, когда один из векторов - (1, 2,.., n), а другой - (n, n-1,.., 1).
Для доказательства рассмотрим выражение 1*a1+2*a2+…+ n*an, где (a1, a2,…, an) - некоторая перестановка чисел 1, 2,…, n.
Пусть для некоторых i и j выполняются соотношения i<j и ai>aj. Тогда, поменяв местами ai и aj мы уменьшим скалярное произведение на (j-i)*(ai-aj).
Учитывая, что 1+4+…+n2 = n*(n+1)*(2n+1)/6, а
1*n + 2*(n-1) +…+ (n-1)*2+n*1 = n*(n+1)*(n*2)/6, окончательно получим, что наибольший угол между векторами будет равен arccos1).
Любопытно, что с ростом n этот угол асимптотически приближается к 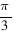 .
.
Награды
Зп правильное решение этой задачки Влад Франк, Макс Алексеев и Вячеслав Пономарев получают по 3 призовых балла.