

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
Конкурс вне Конкурса
В каждой задаче тематического конкурса требовалось указать правило, по которому строится данная последовательность натуральных чисел.
Цена задания определялась в зависимости от количества участников, справившихся с ним.
Условия, Решение и Обсуждение
1) 6, 15, 35, 77, 91, 143, 187, 209,…
Эта последовательность планировалсь как утешительная (утешились не все ;) ) Но есть один нюанс: существует, как минимум, два вполне естественных описания, приводящих к похожим, но разным продолжениям.
а) произведения pq двух простых чисел, таких что p < q < 2p
б) для каждого из последовательных простых чисел p, выписываются его произведения на простые числа q, превосходящие p, не более, чем в 2 раза.
Может показаться, что оба описания задают одну и ту же последовательность, но
на самом деле последовавательности a) и б) будут отличаться порядком членов.
Так, продолжение а) - 221, 247, 299, 323, 391, 437, 493, 527,…
А продолжение б) - 221, 247, 299, 323, 391, 493, 527, 437,…
Конкурсанты предлагали и вариант а), и вариант б). Но никто из них не описал оба продолжения (и не получил дополнительных баллов). Зато встречались описания, не соответствующие приведенным членам :)
Цена задачи - 5 баллов
2) 1, 1, 1, 2, 1, 3, 3, 2, 4, 4, 2, 7, 5, 4, 6, 6, 2, 12, 7, 6, 8, 8, 4, 15, 9, 6, 13,…
Это последовательность троек чисел: f(3n-2) = n, f(3n-1) = φ(n), f(3) = σ(n), где φ(n) - функция Эйлера, а σ(n) - сумма натуральных делителей.
Цена задачи - 6 баллов
3) 71, 431, 719, 1511,…
Эта последовательность допускает несколько описаний, чем и не преминули воспользоваться конкурсанты. При этом авторского описания (простые числа на 10 меньшие квадратов) не предложил никто. Зато были предложены варианты «простые числа вида 36*n*(n+1)-1» и «простые числа, представимые в виде n*(n+4)-6», равносильные авторскому решенеию, а также вариант «простые числа вида 72*n-1, при удалении последней цифры которых они остаются простыми», приводящей к другой последовательности с тем же началом.
Цена задачи - 6 баллов
4) 136, 244, 2178, 6514, 58618, 76438,…
Последовательность состоит из пар чисел:
13 + 33 + 63 = 244, 23 + 43 + 43 = 136;
24 + 14 + 74 + 84 = 6514, 64 + 54 + 14 + 44 = 2178;
55 + 85 + 65 + 15 + 85 = 76438, 75 + 65 + 45 + 35 + 85 = 58618.
Дальше идут числа 2755907 и 6586433, равные суммам 7-х степеней цифр друг
друга.
Эта последовательность предложена Эдвардом Туркевичем. Было это еще в октябре и мне, казалось, что еще тогда я проверил ее на предмет наличия в OEIS. Но только казалось :( Данная последовательность имеется в OEIS по номером A101335.
Цена задачи - 5 баллов (с учетом наличия в OEIS)
5) 2, 5, 11, 19, 30, 44, 62, 85, 115, 155, 210, 288,…
f(n) = n2 + F(n), где F(n) - n-е число Фибоначчи.
В первоначальное условие этого задания вкралсь ошибка. Но это не помешало Матвею Котову справиться с заданием, а заодно указать мне на допущенный ляп и получить бонусные баллы (решившие, в итоге, судьбу первого места).
Цена задачи - 6 баллов
6) 1, 3, 13, 61, 321,…
Эта последовательность оказалась одной из самых интересных.
Авторское решение: f(1) = 1, f(n) = n*f(n-1) + (n-1)2.
Однако возможно и такое описание: 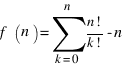 .
И даже такое: f(n) = e*Г(n+1,1) - n.
.
И даже такое: f(n) = e*Г(n+1,1) - n.
Цена задачи - 6 баллов
7) 1, 2, 21, 224, 2521, 31446, 345621, 3845668, 43046721,…
Эта последовательность предложена Алексеем Изваловым. Он верно предположил, что ключом к разгадке может стать последнее из приведенных чисел. В самом деле, бросается в глаза, что 43046721 = 316. Правда, для понимания принципа образования последовательности важнее, что это 98. А общее правило таково: f(n) есть число nn-1, записанное в системе счисления с основанием n+1.
Цена задачи - 7 баллов
8) 2, 65, 72, 128, 250, 370, 468, 520, 637, 730,…
Это числа, каждое из которых представлятся одновременно суммой двух натуральных квадратов и суммой двух натуральных кубов.
Цена задачи - 7 баллов
9) 5, 13, 271, 7159,…
Я полагал, что два последних задания конкурса практически не берутся. Но недооценил интеллектуальной и компьютерной мощи участников конкурса. В частности, не учел того, что в OEIS имеется возможность искать не только «куски» последовательностей, идущие подряд, но и произвольные подпоследовательности.
Последовательность из 9-го задания - это простые числа из A076408. Поясню подробнее. Выпишем натуральные числа, являющииеся нетривиальными (больше первой) степенями натуральных чисел: 1, 4, 8, 9, 16, 25, 27, 32, 36,… Суммируя начальные отрезки этой последовательности будем получать члены A076408. Те из них, которые являются простыми входят в нашу последовательность.
Цена задачи - 7 баллов
10) 7, 13, 15, 21, 26, 31, 40, 42, 43, 57, 62, 63, 73, 80, 85, 86, 91, 93, 111, 114, 121,…
Это числа, которые в некоторой системе счисления записываются набором из не менее чем трех одинаковых цифр. (Ясно, что двумя одинаковыми цифрами записывается любое число, начиная с 2.)
Цена задачи - 7 баллов
ИТОГИ
| Участники | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Σ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Матвей Котов | 5 | 6 | 6 | 5 | 8 | 6 | 7 | 7 | 7 | 7 | 64 |
| 2. | Алексей Волошин | 5 | 6 | 6 | 5 | 6 | 6 | 7 | 7 | 7 | 7 | 62 |
| 3. | Николай Дерюгин | 5 | 0 | 0 | 0 | 6 | 6 | 0 | 0 | 0 | 0 | 17 |
| 4. | Алексей Извалов | 5 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 12 |
| 5. | Виктор Филимоненков | 5 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 11 |
| 6. | Андрей Халявин | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 |
| 6. | Владимир Боровских | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 |
| 8. | Эдвард Туркевич | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 9. | Daogiauvang | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
Учитывая, что первые два призера справились со всеми заданиями и далеко оторвались от преследователей, а также то, что преимущество Матвея перед Алексеем добыто лишь за счет дополнительных показателей, лауретами конкурса объявляются двое: Матвей Котов и Алексей Волошин!
Победителям даруется пожизненное право (и почетная обязанность) бесплатного участия во всех последующих турах Математического марафона! :)