| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№102
Баллы, полученные за решение данной задачи учитываются дважды:
в основном Марафоне и в тематическом конкурсе.
А сама задача является прямым продолжением задач ММ57 и ММ101.
Конкурсная задача №102 (КГ-2) (9 баллов)
На какое наименьшее число частей может разбиваться диагоналями выпуклый n-угольник
при:
a) n = 6;
b) n = 7;
c) n = 8;
d) n = 9?
Примечание:
Цена задачи указана весьма условно.
Я умею строго обосновывать минимальность известных мне разбиений не для всех указанных n.
Соответственно и сами известные мне ответы могут оказаться неверными.
9 призовых баллов будет присуждаться за решения аналогичые моему (имеющие тот же
ответ и ту же степень строгости его обоснования).
За улучшение известных мне ответов, получение более строгих обоснований, получение
(хотя бы частично) обоснованных ответов для бОльших n будут начисляться дополнительные
призовые баллы.
Решение
Будем называть диагонали, соединяющие вершины выпуклого многоугольника через одну «короткими»), через две - «средними», через три - «длинными». Точку внутри многоугольника будем называть особенностью порядка k, если в ней пересекаются k+2 диагоналей. Ясно, что особые точки могут возникать только при пересечении средних и длинных диагоналей.
Ординарный n-угольник разбивается своими диагоналями на (n-1)(n-2)(n2-3n+12)/2 частей, что при интересующих нас n составляет 25, 50, 91 и 154 соответственно. Каждая особенность порядка k уменьшает количество частей разбиения на k(k+1)/2. Сумму этих чисел по всем особенностям будем называть дефектом многоугольника. Для решения задачи нужно найти максимальный дефект для каждого из данных n.
a) У шестиугольника всего 3 диагонали, не являющихся короткими. Поэтому в шестиугольнике может возникнуть всего одна особенность порядка 1 (она есть, например, в правильном шестиугольнике). Соответственно максимальный возможный дефект шестиугольника - 1 и минимально возможное число частей разбиения - 24.
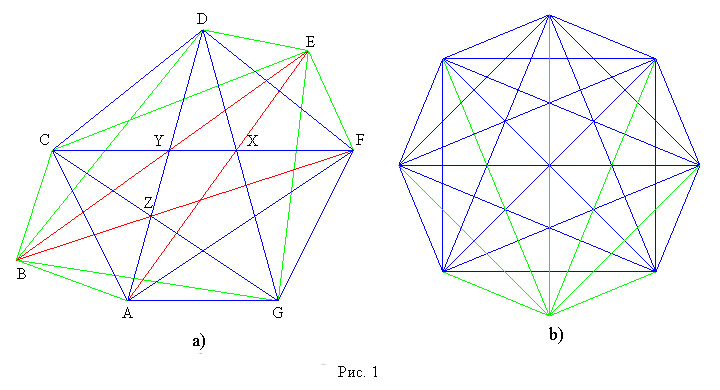
b) У семиугольника не может быть особенностей, порядок которых больше 1, (вершин не хватает). А то, что число осбенностей первого порядка не может превышать 3, следует из рассуждений, приведенных в решении задачи ММ104. В то же время 3 особых точки возможны. На рисунке 1 приведены два способа получения семиугольника с тремя особыми точками: достроением правильного пятиугольника; удалением вершины правильноо восьмиугольника. Разумеется, существуют и подходящие семугольники никак не связанные с правильными многоугольниками.
Итак, максимальный дефект семиугольника - 3, наименьшее возможное число частей разбиения - 47.
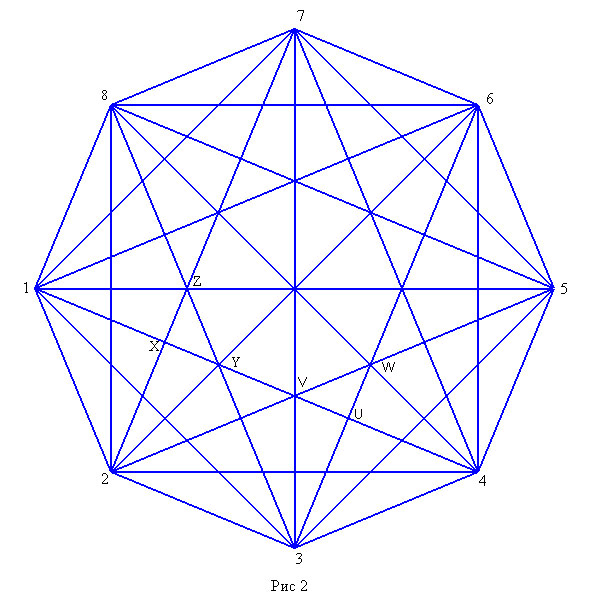
c) Представляется очевидным, что максимальный возможный дефект восьмиугольника возникает (в частности) у правильного восьмиугольника. Докажем это утверждение. При наличии особенности второго порядка на средней диагонали не может быть больше двух особенностей. Это легко увидеть на рисунке 2.
На средней диагонали 1-4 уже есть две особенности Y и V. Точки пересечения нашей диагонали с короткими диагоналями не могут быть особенными. Остаются два кандидата на особые точки. Это X и U. Cделать точку X особой можно за счет смещения диагонали 3-8. Но это неизбежно приведет к тому, что точка Y, а заодно и Z перестанут особыми. Аналогично обстоят дела с точкой V. Поэтому на средней диагонали восьмиугольника не может быть больше двух особых точек. Но у правильного восьмиугольника на каждой средней диагонали их ровно по две. Единственная особенность второго порядка может возникать только на пересечении всех длинных диагоналей восьмиугольника. И у правильного восьмиугольника такая особенность есть. Таким образом, правильный восьмиугольник обладает максимальным дефектом среди всех восьмиугольников: он имеет 8 особых точек первого порядка и одну особую точку второго порядка. Поэтому дефект правильного восьмиугольника - 11, а число частей разбиения 80.
d) Именно к этому пункту относилось примечание к условию. Мне удалось найти
девятигольник с дефектом 17. Я полагаю, что это максимальный возможный
дефект, но доказывать это не умею.
Как и все конкурсанты, бравшиеся за задачу ММ102, я стартовал с правильного
восьмиугольника. Поместим вершины правильного восьмиугольника на единичной
окружности, в точках с координатами (cos(Π·i/4); sin(Π·i/4),
где i ∈ {0,1,…,7}. В качестве девятой вершины возьмем точку с
координатами ((-4-√2)/6; (4-√2)/6) (она тоже лежит на
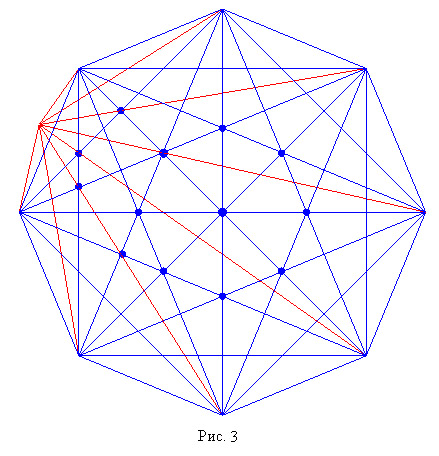
единичной окружности). Не сложно убедиться, что жирные синие точки на рисунке 3
являются особыми, а две наиболее крупные из них - особенности второго порядка.
Поэтому дефект нашего девятиугольника равен 17, а число частей разбиения - 137.
Обсуждение
Представляется правдоподобной гипотеза: при четных n максимальный дефект имеют
правильные n-угольники. Другое утверждение «правильные n-угольники с нечетным
числом сторон ординарны» относительно недавно перекочевало из разряда
правдоподобных предположений в категорию теорем. Набросок доказательства
появился еще в 1936 году в статье G.Bol: Beantwoording van prijsvraag no.17,
Nieuw Archief voor WisKunde 18 (1936), p.14-66.
Но строгое доказательство было опубликовано лишь в 1998 году: см.
«The number of intersection points made by the diagonals of a regular polygon»,
B. Poonen, M. Rubinstein, SIAM J. on Discrete Mathematics, Vol. 11, No. 1
(1998), p. 135-156.
В этой статье выведена формула для количества частей разбиения правильного
n-угольника при любом n. Оказывается, за исключением центра, никакая особенность
правильного n-угольника не может иметь порядок выше 5, а особенности пятого
порядка (отличные от центра) впервые встречается в правильном 30-угольнике.
В целом же формула для числа частей разбиения распадается на 2520 случаев
(которые авторам не без изящества удалось запихнуть в одну не слишком
громоздкую формулу).
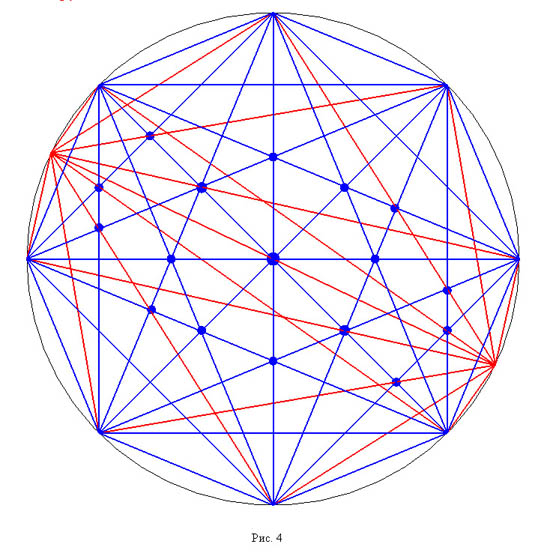
Если принять гипотезу о том, что правильный десятиугольник - «наиболее дефективный» среди десятиугольников, можно получить еще одно косвенное подтверждение тому, что построенный нами девятиугольник имеет максимальный возможный дефект. Добавив к нашему девятиугольнику вершину, симметричную девятой вершине относительно центра исходного восьмиугольника (см. рис. 4), получим десятиугольник с дефектом 26, т.е. с таким же дефектом. как у правильного десятиугольника.
Андрей Халявин нашел для дефекта девятиугольника некоторую оценку сверку. Но она безусловно сильно завышена (28).
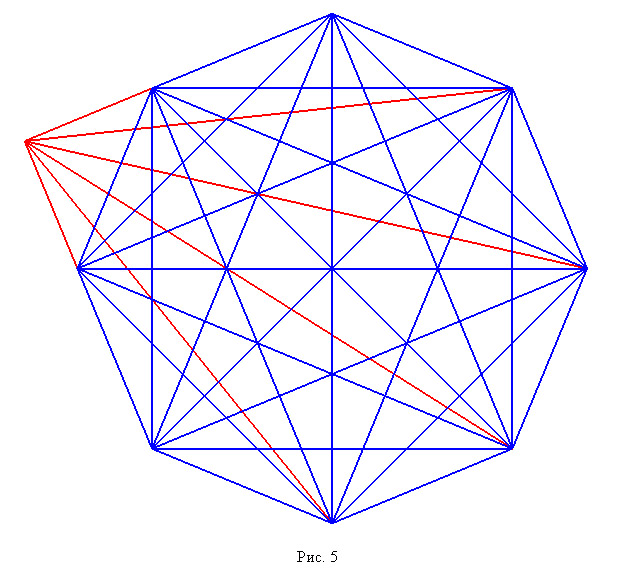
Анатолий Казмерчук тоже нашел было девятиугольник с дефектом 17, но при ближайшем рассмотрении этот объект оказался то ли не совсем выпуклым, то ли не совсем девятиугольником (см. рис. 5).
Награды
Андрей Халявин и Анатолий Казмерчук (нашедшие девятиугольники с дефеком 15) получают по 8 призовых баллов. Николай Дерюгин нарисовал девятиугольник разрезаный 137 частей и поразительно похожий на тот, что приведен на рисунке 3 (только красиво раскрашенный), но не снабдил свою картинку обоснованиями (более строгими чем «похоже, что…»). Кроме того, он не обосновал максимальность дефекта правильного восьмиугольника. Николай получает 6 призовых баллов.
Эстетическая оценка задачи - 5 баллов