| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№104
Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задач ММ57, ММ101, ММ102 и ММ103.
Конкурсная задача №104 (КГ-4) (9 баллов)
Два выпуклых n-угольника назовем изоморфными, если изоморфны их сопровождающие графы.
Два выпуклых n-угольника назовем однотипными, если в разбиениях этих многоугольников на элементарные присутствует поровну треугольников, поровну четырехугольников и т.д.
1. Имеется ли логическая зависимость между однотипностью и изоморфностью
выпуклых многоугольников?
2. На сколько классов однотипных семиугольников разбиваются ординарные
семиугольники?
3. На сколько классов изоморфных семиугольников разбиваются ординарные
семиугольники?
Решение
1. Очевидно, что и однотипность и изоморфность являются отношениями эквивалентности на множестве ординарных n-угольников. Степень каждой вершины сопровождающего графа равна количеству сторон соответствующего элементарного многоугольника (исключение составляют n элементарных треугольников, у которых одна из сторон является стороной исходного n-угольника). Поскольку степени соответствующих вершин изоморфных графов равны, очевидно, что изоморфные многоугольники являются одновременно и однотипными. То, что обратное утверждение не имеет места будет видно из рассмотрения последующих пунктов.
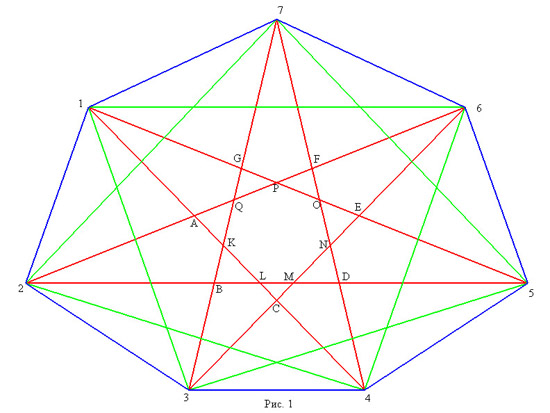
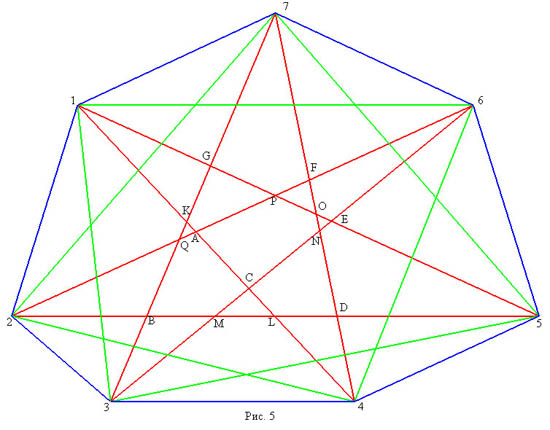
2-3. Диагонали выпуклого семиугольника, соединяющие вершины через одну, будем называть «короткими», а остальные - «длинными». На рисунках короткие диагонали изображены зеленым цветом, а длинные - красным. Короткие диагонали высекают из исходного семиугольника внутренний семиугольник, содержащий 22 элементарных многоугольника (эти элементарные мнооугольники, а также точки пересечения длинных диагоналей мы тоже будем называть внутренними). Остальные 28 элементарных многоугольников (будем называть образованную ими часть семиугольника «периферийной») для любого ординарного (и даже для любого выпуклого) семиугольника являются треугольниками. Строение периферийной части одинаково для всех выпуклых семиугольников. Учитывая это, договоримся при изображении сопровождающего графа, рисовать только 22-вершинный подграф, порожденный внутренними элементарными многоугольниками. (В то же время, исходные семиугольники будем рисовать целиком.)
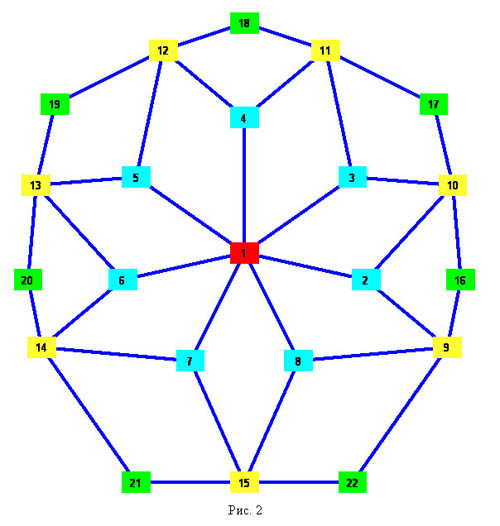
Стартуем с рассмотрения семиугольника, изоморфного (а значит, и однотипного) правильному. Он изображен на рисунке 1, а внутренняя часть его сопровождающего графа - на рисунке 2 (голубым цветом изображены вершины, соответствующие треугольникам; зеленые - четырехугольникам; желтые - пятиугольникам; красная - семиугольнику).
Пронумеруем вершины семиугольника и введем обозначения для точек пересечения длинных диагоналей: А - на пересечении диагоналей 1-4 и 2-6 и т.д. (см. рисунок 1). Те из внутренних точек, которые являются вершинами элементарного семиугольника, дополнительно будем называть «центральными», а остальные внутренние точки - «окаймляющими».
Деформируя наш семиугольник, мы можем поменять строение сопровождающего графа только за счет изменения взаимного расположения внутренних точек. Например, смещая вешршины 3 и/или 7, можно добиться, чтобы диагональ 3-7 оказалась по другую сторону от точки A. Аналогичного эффекта можно добиться для других окаймляющих точек. Но некоторые такие «перетаскивания» несовместимы. Если мы перетаскиваем соответствующую диагональ за одну из окаймляющих точек, то мы не можем проделать то же самое с соседними окаймляющими точками. Так, перетаскивая диагональ 3-7 за точку A, мы лишаем себя возможности, перетащить диагональ 1-4 за точку B и диагональ 2-6 за точку G. Поэтому элементарный семиугольник можно лишить не более чем трех вершин.
Учитывая вышеизложенное мы легко можем перечислить все классы изоморфных ординарных семиугольников.
1. Семиугольники, изморфные правильному. Такой семиугольник и центральную часть его сопровождающего графа мы уже рассмотрели (рис. 1-2). У таких семиугольников разбиение состоит из 28+7 треугольников, 7 четырехугольников, 7 пятиугольников и одного семиугольника.
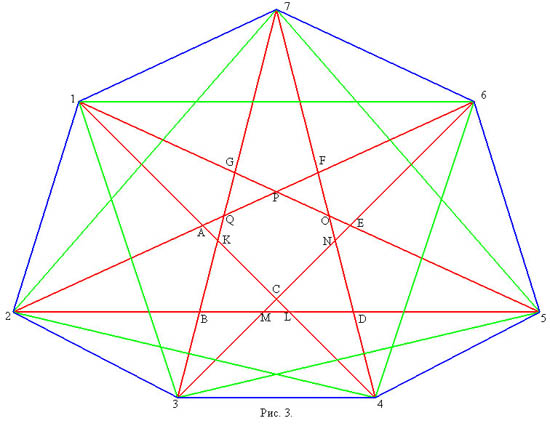
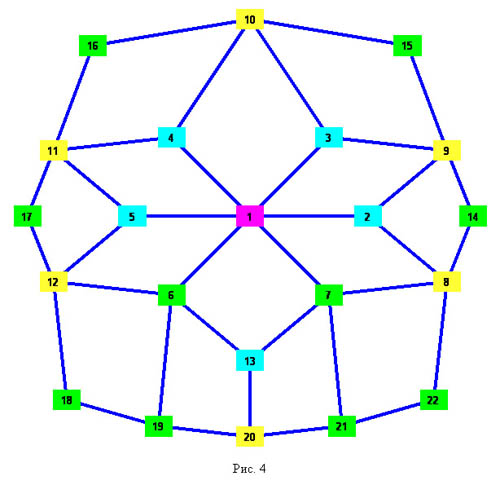
2. Семиугольники полученные из семиугольников первого класса перетаскиванием одной (из соображений симметрии все равно какой) длинной диагонали за окаймляющую точку. На рисунке 3 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C, а на рисунке 4 - центральная часть его графа. У таких семиугольников разбиение состоит из 28+5 треугольников, 10 четырехугольников, 6 пятиугольников и одного шестиугольника.
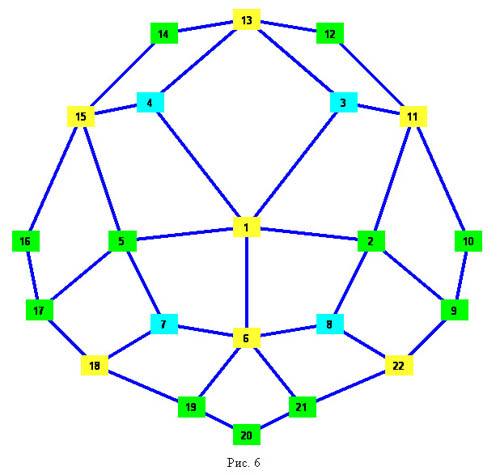
3. Семиугольники полученные из семиугольников первого класса перетаскиванием двух диагоналей за окаймляющие точки, раположенные через одну. На рисунке 5 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C и диагонали 3-7 за точку A. На рисунке 6 приведена внутренняя часть сопровождающего графа. У таких семиугольников разбиение состоит из 28+4 треугольников, 11 четырехугольников и 7 пятиугольников.
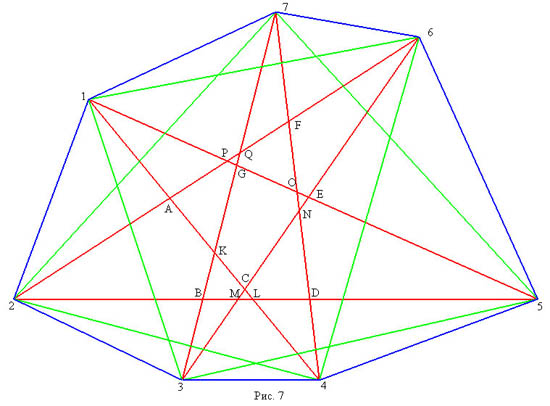
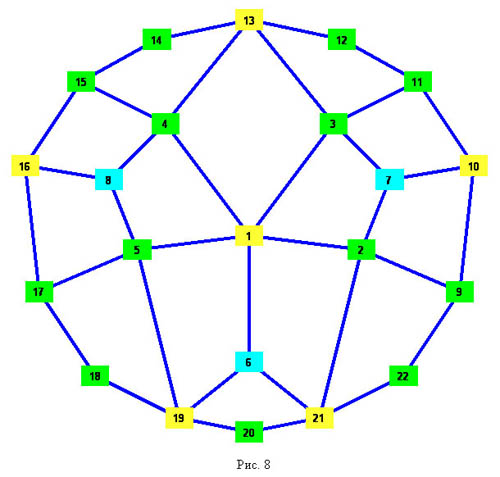
4. Семиугольники полученные из семиугольников первого класса перетаскиванием двух диагоналей за окаймляющие точки, раположенные через две. На рисунке 7 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C и диагонали 2-6 за точку G. На рисунке 6 приведена внутренняя часть сопровождающего графа. У таких семиугольников разбиение состоит из 28+3 треугольников, 13 четырехугольников и 6 пятиугольников.
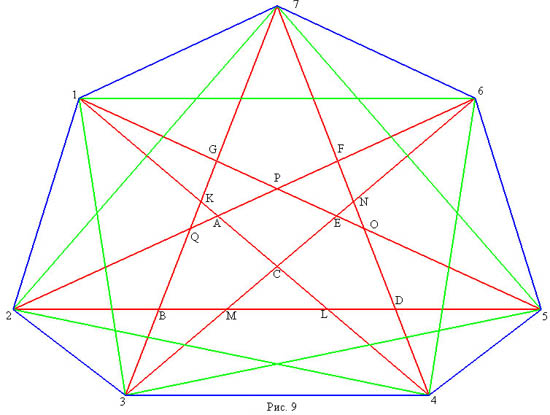
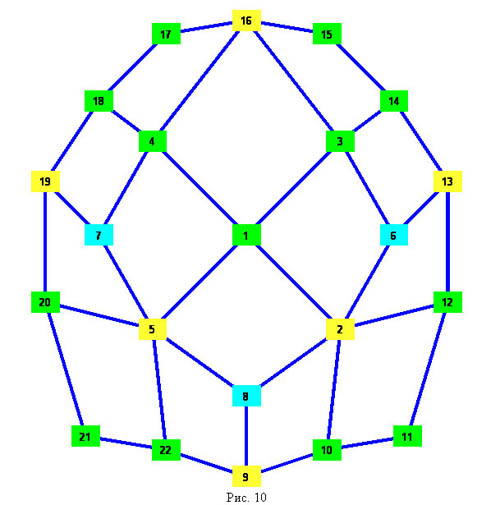
5. Семиугольники полученные из семиугольников первого класса перетаскиванием трех диагоналей за окаймляющие точки. На рисунке 9 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C, диагонали 3-7 за точку A и диагонали 4-7 за точку Е. Внутренняя часть сопровождающего графа приведена на рисунке 10. У таких семиугольников разбиение состоит из 28+3 треугольников, 13 четырехугольников и 6 пятиугольников.
Семиугольники из последних двух классов оказались однотипными. В то же время, их сопровождающие графы, очевидно, не изоморфны (напрмер, у одного из них во внутренней части есть вершины степени 3, удаленные друг от друга на 2, а у другого - нет).
Таким образом, имеется 5 классов изоморфных и 4 класса однотипных ординарных семиугольников.
Обсуждение
А налогичная классификация ординарных (или любых выпуклих) n-угольников для бОльших представляется весьма трудной (хотя, по крайней мере, при n = 8 вполне посильной) задачей.
Награды
За правильное решение этой задачи Анатолий Казмерчук получает 9 призовых баллов.
Эстетическая оценка задачи - 5 баллов