

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№108
Задачка с антресолей.
Конкурсная задача ММ108 (4 балла)
Однородную пирамиду разрезали на слои равной толщины плоскостями, параллельными основанию. При каком наименьшем количестве частей их можно будет разложить на разные чаши равноплечных весов без гирь так, чтобы весы уравновесились?
Решение
Приведу решение Алексея Волошина.
Пусть вес самой верхней части (самой маленькой) равен 1. Тогда, из соображений подобия вес первых k частей равен k3, а вес k-го слоя равен k3-(k-1)3.
Следовательно, вес каждого слоя - целое число. Если их можно разложить на разные чаши равноплечных весов без гирь так, чтобы весы уравновесились, то общий вес пирамиды - чётное число. Следовательно, общее число слоёв должно быть чётно.
При разбиении на 2 части на каждую чашу весов необходимо положить вес (23)/2=4, а веса слоёв равны 1 и 7. Вес второго слоя превышает 4, следовательно, уравновесить весы нельзя.
При разбиении на 4 части на каждую чашу весов необходимо положить вес (43)/2=32, а веса слоёв равны 1, 7, 19, и 37. Вес четвертого слоя превышает 32, следовательно, уравновесить весы нельзя.
При разбиении на 6 частей на каждую чашу весов необходимо положить вес (63)/2=108, а веса слоёв равны 1, 7, 19, 37, 61 и 91. На одну из чаш мы положим последний слой весом 91. Дополнительно на эту чашу нужно положить слои суммарным весом 108-91=17. Но слои весом более 17 мы положить не сможем, а вес всех оставшихся частей равен 1+7=8, т. е. меньше 17. Следовательно, уравновесить весы нельзя.
При разбиении на 8 частей на каждую чашу весов необходимо положить вес (83)/2=256, а веса слоёв равны 1, 7, 19, 37, 61, 91, 127 и 169. Имеем:
1+37+91+127=7+19+61+169=256.
Ответ: наименьшее количество слоёв равно 8.
Обсуждение
Задача ММ108 имеет интересное обобщение. Порежем n-мерную пирамиду гиперплоскостями,
параллельными гиперплоскости основания на 2n слоев равной толщины. Тогда
т-мерные объемы слоев будут относиться как разности соседних n-x степеней.
Оказывается, при любом n можно разбить полученные слои на два класса по
2n-1
кусков в каждом, так что суммарные n-мерные объемы кусков в классах будут равны.
Пронумеруем куски от вершины к основанию числами 0, 1, …, 2n-1.
Соответствующее разбиение задается производящей функцией:
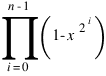 . Если (после раскрытия скобок) коэффициент при
соответствуещей степени x положителен помещаем кусок в первый класс, если
отрицателен - во второй.
. Если (после раскрытия скобок) коэффициент при
соответствуещей степени x положителен помещаем кусок в первый класс, если
отрицателен - во второй.
Альтернативный способ - поместить в первый класс те и только те куски, номера
которых в двоичной записи содержат четное число единиц.
Я надеялся, что участники Марафона выйдут на вышеописанное обобщение и уже изготовился щедро раздавать дополнительные призовые баллы. Однако дождался лишь намека на обобщение от Тимофея Игнатьева.
Полагаю, эстетическая оценка задачи была бы выше, если бы учаастники Марафона оценивали задачу с учетом обобщения на произвольное n.
Для n ≤ 3 2n - наименьшее число слоев, удовлетворяющее условию. Будет ли оно таковым для бОльших n мне неизвестно.
Награды
За правильное решение задачи ММ108 Тимофей Игнатьев получает 5 призовых баллов, а Виктор Филимоненков, Кирилл Веденский, Алексей Волошин, Николай Дерюгин и Анатолий Казмерчук - по 4 призовых балла.
Эстетическая оценка задачи - 3.8 балла