| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№117
Задача ММ117 утратила статус конкурсной и может свободно обсуждаться.
Призовые баллы за решение ММ117 учитываются дважды: в тематическом конкурсе и в основном Марафоне. А сама задача ММ117 является прямым продолжением задачи ММ115 и так же как ММ115 предложена Сергеем Половинкиным.
Конкурсная задача ММ117 (Ш-4) (7 баллов)
На шахматной доске расставлено 64 белых коня. Какое минимальное количество коней нужно заменить черными, так чтобы в полученной позиции, действуя по правилам задачи ММ115, было бы невозможно получить хотя бы один одноцветный квадрат 5Х5? Каково количество таких позиций?
Решение
Приведу решение Дмитрия Пашуткина.
Очевидно, что одного чёрного коня недостаточно.
Покажем, что два чёрных коня можно расположить так, чтобы получить одноцветный белый квадрат было нельзя и заодно найдем количество таких размещений чёрных коней.
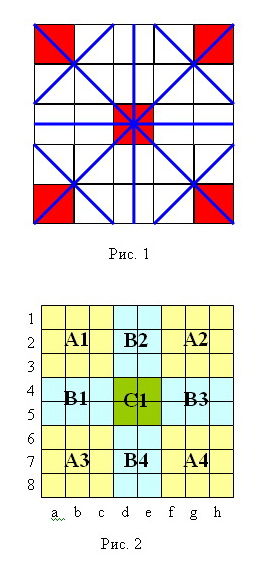
Сначала заметим, что если чёрные кони (один или оба) стоят на выделенных красным цветом полях, то такой квадрат можно преобразовать к одноцветному.
Для угловых полей это очевидно. Цвет всех полей, кроме центрального, можно поменять на противоположный, если выполнить преобразования по синим линиям на рис. 1:
Разобьём доску на несколько областей (рис. 2):
Рассмотрим варианты расположения 2-х черных коней на доске.
Если оба коня находятся в жёлтой области, то на доске останется белый квадрат 5х5.
Пусть один из чёрных коней стоит на жёлтой области. Не теряя общности, можно считать, что конь стоит в квадрате A1. Покажем, что в этом случае всегда можно построить белый квадрат. Действительно, если второй конь не стоит в области C1, то обязательно останется белый квадрат 5х5. Если же второй конь находится в области C1, то он может располагаться либо в клетках d4,d5,e4 и тогда он будет находиться в угловой клетке белого квадрата 5х5, либо в клетке e5 и тогда получим белый квадрат 5х5 с черным конем в центре (e5) и возможно в углу (зависит от расположения первого коня в жёлтом поле). В любом из этих случаев можно построить белый квадрат 5х5.
Т.о. если хотя бы один черный конь стоит в желтой области, то белый квадрат можно построить.
Если оба коня расположены в одной голубой области, то очевидно останется белый квадрат.
Пусть один чёрный конь расположен в одной голубой области, а второй конь - в другой голубой области. Не теряя общности, можно считать, что первый конь стоит в области B1. Если второй конь расположен в области B2 или B4, то на доске останется белый квадрат. Если же второй конь расположен в области B3, то первый конь может располагаться в клетках c4 или c5 и можно выделить белый квадрат 5х5 с чёрным центром в этой клетке, или первый конь стоит в других клетках области B1 и тогда можно построить белый квадрат с черными конями в угловых клетках.
Т.о. если оба коня стоят в голубой области, то белый квадрат также всегда можно построить.
Осталось рассмотреть 2 случая: оба чёрных коня находятся в квадрате С1; один конь голубой в области, а другой в C1.
Пусть оба коня находятся в области C1. Тогда с точностью до поворота возможно два варианта расположения коней.
Первый изображен на рисунке 3:
В этом случае очевидно можно построить белый квадрат.
Второй вариант расположения коней показан на рисунке 4:
Воспользовавшись идеей из обсуждения решения задачи 115, расположим на доске восьмиклеточные конфигурации так, чтобы в каждой конфигурации было ровно по одному чёрному коню. Любой квадрат 5х5 содержит как минимум одну конфигурацию (для проверки удобно передвигать по доске выделенный квадрат 5х5). Т.о. при таком расположении коней одноцветный квадрат получиться не может, и с учётом симметрии получим 4 варианта расположения коней, при которых построение одноцветного квадрата 5х5 невозможно.
Рассмотрим последний возможный вариант - один конь в голубой области, один конь в квадрате С1. В этом случае получаем с точностью до симметрии два варианта (рис.5 и рис. 6), когда построение одноцветного квадрата 5х5 невозможно:
Каждое расположение даст по 8 вариантов.
При других комбинациях получим либо квадрат с конем в угловой клетке, либо квадрат с конем в центральной клетке.
Суммируя полученные результаты, заключаем: достаточно двух черных коней, вариантов их расположения 20.
Обсуждение
Назовем две расстановки коней в каждом поле доски эквивалентными, если каждую из них можно получить из другой допустимыми преобразованиями.
Легко видеть, на доске 4х4 существует два класса эквивалентных между собой расстановок.
Эдвард Туркевич поставил вопрос о количестве классов для доски 8х8, Сергей Половинкин утверждает, что в этом случае классов не менее 64.
Награды
За составление задачи ММ117 Сергей Половинкин получает 7 призовых баллов. По столько же баллов за правильное решение задачи получают Алексей Волошин, Эдвард Туркевич, Анатолий Казмерчук и Дмитрий Пашуткин. Николай Дерюгин получает 4 призовых балла.
Эстетическая оценка задачи - 4.5 балла