| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№120
Задача ММ120 утратила статус конкурсной и может свободно обсуждаться на форуме.
Задача ММ120 продолжает линию задачи ММ57 и тематического конкурса 11-го тура.
Конкурсная задача ММ120 (7 баллов)
В задаче ММ103 каждому выпуклому многоугольнику был поставлен в соответствие сопровождающий граф: вершины графа - элементарные многоугольники, на которые разбивается исходный многоугольник своими диагоналями; две вершины смежны, если соответствующие многоугольники имеют общую сторону.
Найти возможные значения диаметра и радиуса, а также возможные количества периферийных и центральных вершин сопровождающего графа произвольного выпуклого n-угольника.
Решение
Легко видеть (и доказать), что расстояние между двумя вершинами сопровождающего графа равно количеству диагоналей исходного многоугольника, разделяющих элементарные многоугольники, соответствующие данным вершинам.
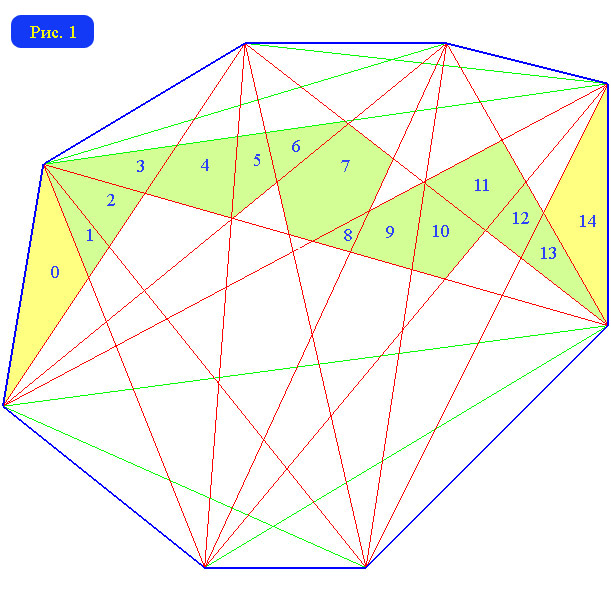
С периферийными вершинами и диаметром дело обстоит достаточно просто. Легко понять, что периферийными вершинами сопровождающего графа будут элементарные треугольники, имеющие общую сторону с исходным многоугольником. При четном n наиболее удаленными друг от друга вершинами графа будут элементарные треугольники, примыкающие к противоположным сторонам исходного n-угольника (рис. 1), а при нечетном - к «наиболее противоположным». Простой комбинаторный подсчет количества диагоналей, разделяющих такие элементарные треугольники, дает следующие значения диаметра: D=(n2-8)/4 для четных n и D=(n2-9)/4 - для нечетных.
Итак, количество периферийных вершин и диаметр сопровождающего графа зависят только от числа сторон исходного многоугольника, а именно: диаметр равен [(n2-8)/4], а число периферийных вершин сопровождающего графа равно n (при n>3).
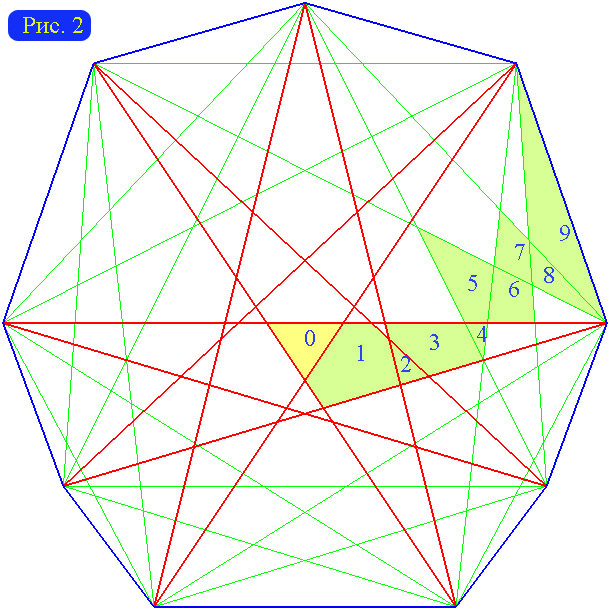
Гораздо сложнее обстоит дело с радиусом и центральными вершинами сопровождающих графов. Достаточно просто определить лишь наименьшее значение радиуса. Сначала оратимся к исходным многоугольникам с нечетным числом сторон (n=2k+1, k - натуральное). В этом случае для каждого k существует многоугольник, радиус которого равен R=(n2-9)/8, т.е. половине диаметра. Это верно, например, для правильных многоугольников. Диагонали многоугольника с нечетным числом сторон, соединяющие вершину с концами противолежащей стороны, будем называть «большими». Треугольники, высекаемые парами больших диагоналей, выходящих из одной вершины исходного многоугольника, будем называть «центральными секторами». В общем случае радиус сопровождающего графа нечетноугольника будет равен половине диаметра тогда и только тогда, когда существует элементарный многоугольник, лежащий внутри всех центральных секторов. На рисунке 2 такой элементарный многоугольник закрашен желтым цветом, а большие диагонали выделены красным. Если такой элементарный многоугольник существует, то он является единственной центральной вершиной сопровождающего графа.
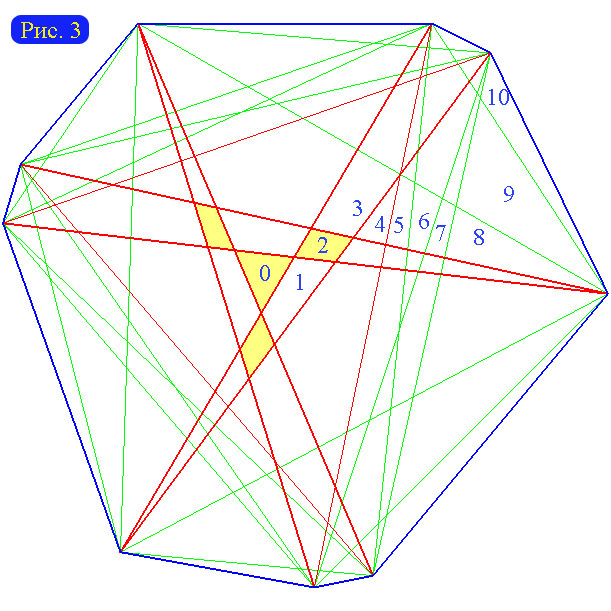
Заметим, что наши рассуждения будут верны и для k = 1. В этом случае «большими диагоналями» будут стороны треугольника, а сам треугольник будет центральным сектором для каждой своей вершины. Однако, начиная с k=4, элементарный многоугольник, принадлежащий всем центральным секторам может и не существовать. На рисунке 3 представлен такой девятиугольник. Элементарные многоугольники, являющиеся центральными вершинами сопровождающего графа, выделены желтым цветом. Обратите внимание, что по пути из каждой центральной вершины в наиболее отдаленную от нее приходится преодолевать пять больших диагоналей (а для девятиугольника на рисунке 2 хватало четырех).
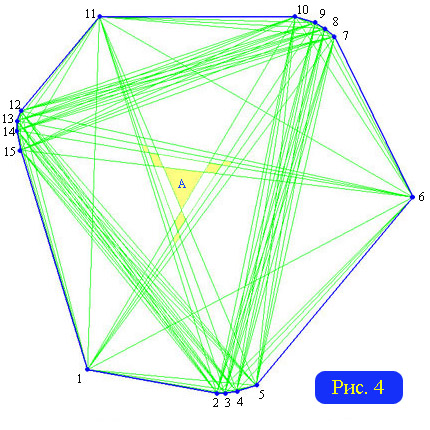
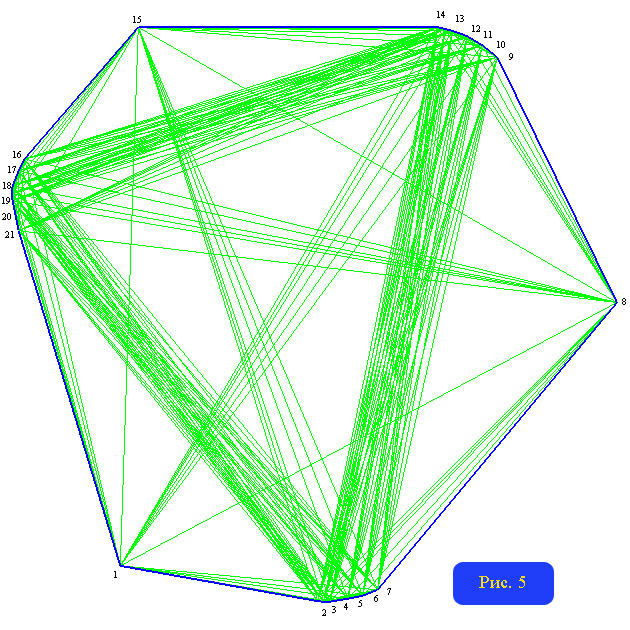
Используя тот же подход (назовем его «методом децентрации»), при подходящих k можно добиться сколь угодно большого превышения радиусом значения D/2. Для этого подходят многоугольники, у которых не только большие диагонали, но и примыкающие к ним образуют секторы. имеющие пустое пересечение. На рисунке 4 представлен 15-угольник, радиус сопровождающего графа которого равен 30, т.е. на 3 превосходит половину диаметра. 7 центральных вершин выделены желтым цветом. Если же число сторон исходного многоугольника увеличить до 21, то можно построить многоугольник с радиусом графа равным 60, что на 6 больше половины диаметра. На рисунке 5 представлен такой многоугольник (10 элементарных многоугольников, соответствующих центральным вершинам, цветом не выделены из-за малых размеров).
Обобщая случаи n=9, n=15, n=21, придем к выводу, что при n=6k+3 существует многоугольник, сопровождающий граф которого имеет радиус 5k(k+1) и 3k+1 центральных вершин. Я полагаю, что именно для многоугольников с числом сторон 6k+3 имеет место наибыстрейший рост максимального радиуса, но точного доказательства этого факта у меня нет. Если n не сравнимо с 3 по модулю 6, то радиус растет не так быстро, но сама идея децентрации, все равно, работает. Например, убрав пару вершин у 21-угольника с рисунка 5, можно получить 19-угольник, у которого радиус превышает половину диаметра на 3.
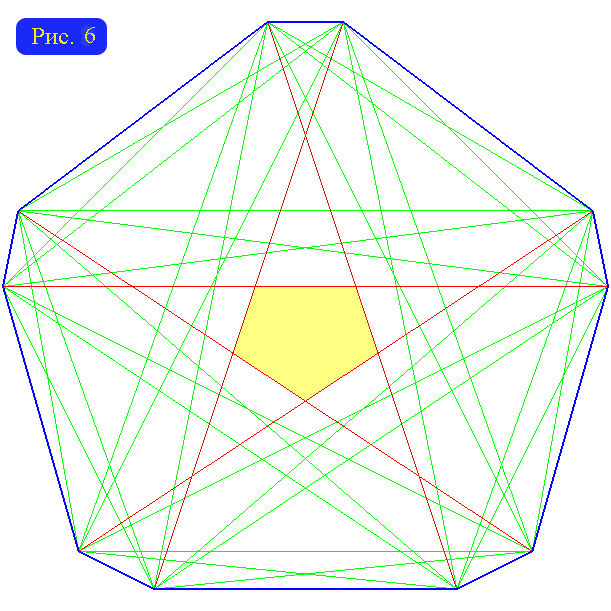
Перейдем к рассмотрению сопровождающих графов многоугольников с четным числом сторон. Первым делом докажем, что в этом случае радиус не может равняться половине диаметра. Для n=4k+2 это очевидно в силу нечетности диаметра. Но значение R=(n2-4)/8 в этом случае достижимо. Для получения подходящего многоугольника достаточно отрезать уголки у правильного многоугольника с нечетным числом сторон (рис.6).
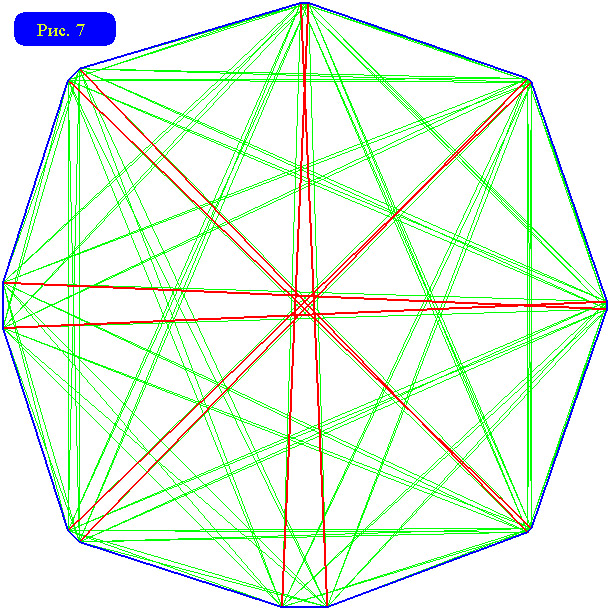
Пусть теперь n=4k. Положим r=D/2. Допустим, что у графа 4k-угольника есть вершина с эскцентриситетом r. Тогда расстояние от этой вершины каждой периферийной вершины должно равняться r: Оно не может быть больше r, поскольку r - это эксцентриситет, а если хотя бы одна периферийная вершина удалена меньше чем на r, то диаметр будет меньше 2r. Но расстояния от любой вершины до периферийных вершин, примыкающих к соседним сторонам исходного многоугольника, имеют разную четность (в одном случае надо пересекать большую диагональ, выходящую из общей для данных сторон вершины многоугольника, а в другом - нет). Полученное противоречие доказывает наше утверждение. Наименьшим значением радиуса для n=4k будет R=D/2+1=n2/8. Подходящий 4k-угольник можно получить из правильного 2k-угольника, отрезав от него маленькие уголки: k совсем малюсенькиx, а k других чуть побольше (см. рис.7)
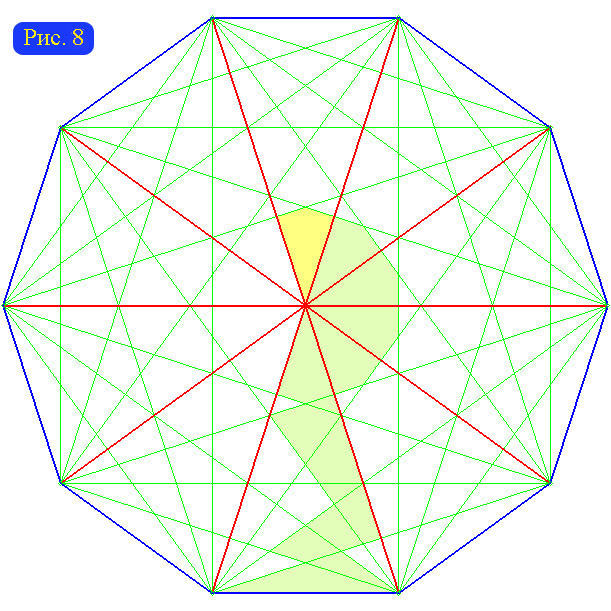
Большие диагонали многоугольника с четным числом сторон (n=2k) могут пересекаться в одной точке (например, в правильном многоугольнике). Это приводит к образованию в сопровождающем графе цикла длины n. Необходимость «обходить эту дыру» (см. рис. 8) приводит к увеличению радиуса на [n/4].
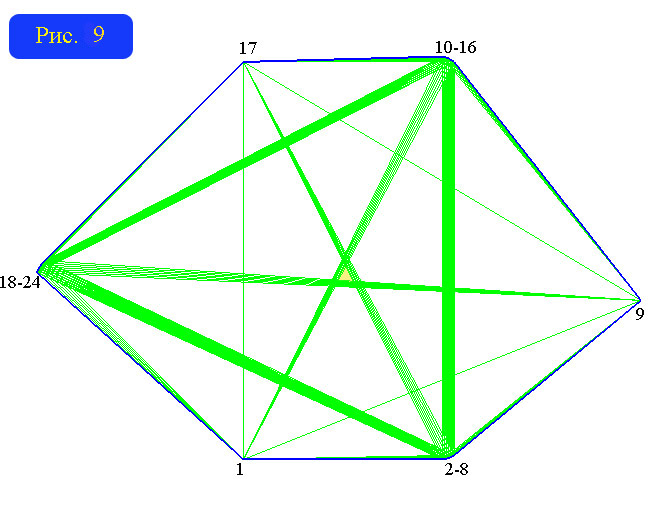
Гипотеза, высказанная несколькими конкурсантами (к ней склонялся и я на ранней стадии составления задачи), «наибольшее значение радиуса сопровождающего графа 2k-угольника достигается для правильных многоугольников и равно (n^8+2n-8)/8» НЕ ВЕРНА для почти всех k. Ведь превышение радиуса над половиной диаметра растет для графов правильных 2k-угольников линейно относительно числа сторон, в то время как метод децентрации (а он применим и для разбираемого случая), дает рост по квадратичному закону. Впервые четноугольник, построенный по методу децентрации, приводит к графу, радиус которого превышает радиус графа правильнгого многоугольника с тем же числом сторон при n = 24. Посмотреть (но не рассмотреть :)) его можно на рисунке 9. Его радиус (равный, например, расстоянию от желтого элементарного треугольника в центре, до элементарного треугольника, примыкающего к стороне 5-6) равен 79, в то время как радиус графа правильного 24-угольника равен 77.
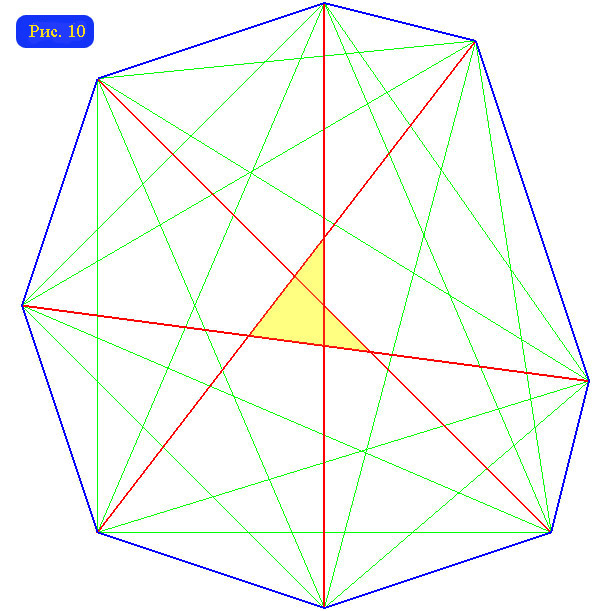
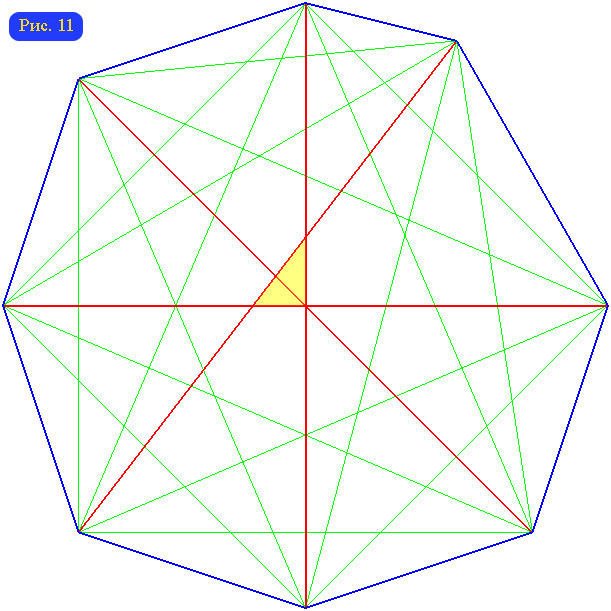
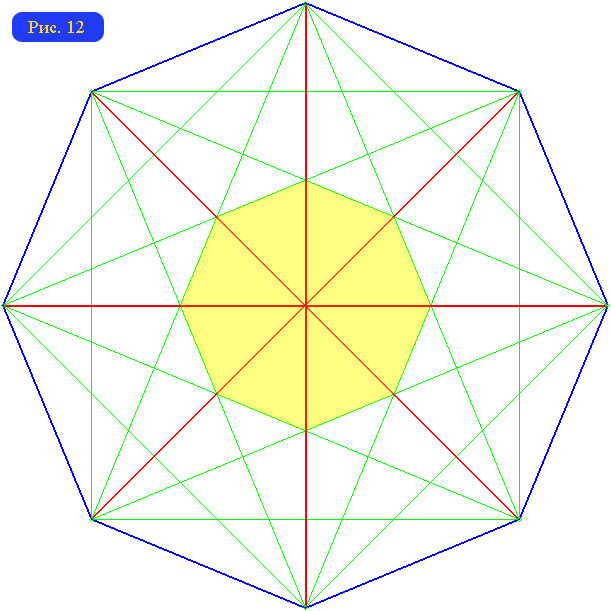
Ситуация с центральными вершинами достаточно сложна. Единственную центральную вершину имеют графы треугольников, пятиугольников и семиугольников. У графа четырехугольника все 4 вершины центральные. Для остальных n количество центральных вершин может быть различным. Например, у графа шестиугольника одна либо шесть центральных вершин. А у графа восьми угольника может быть две, три или восемь центральных вершин (см. рис. 10-12). Для общего случая справедливы такие утверждения: При n, не кратном 4, существуют многоугольник, граф которого имеет единственную центральную вершину; При четном n существует многоугольник, граф которого имеет n центральных вершин. Больше чем n центральных вершин граф n-угольника иметь, по-видимому, не может.
Обсуждение
Единственную центральную вершину может иметь и граф 12-угольника. 16-угольников с таким свойством я не нашел. Не исключено, что графа с единственной центральной вершиной не существует тогда и только тогда, когда число сторон соответствующего многоугольника - степень двойки.
Анонсируя задачу, я заявил, что она имеет прямое отношение не только к ММ57 и к тематическим задачам 11-го тура, но и еще к одной марафонской задаче. Чтобы убедиться в справедливости этого утверждения достаточно сравнить выражение для диаметра сопровождающего графа с верхней гранью диапазона отношения суммы длин диагоналей к периметру выпуклого многоугольника, вычисленной в задаче ММ2 (см. Архив Марафона).
Анатолий Казмерчук предложил красивую формулу для определения расстояния между вершинами сопровождающего графа: Занумеруем (например, против часовой стрелки) n вершин исходного многоугольника. Занумеруем (например, слева направо, если смотреть от вершины) секторы, на которые разбивают исходных многоугольник, диагонали исходящие из данной вершины. Каждому элементарному многоугольнику поставим в соответствие уникальный набор из n индексов, соответствующих секторам, в которые он попал. Тогда расстояние между элементарными многоугольниками (вершинами сопровождающего графа) будет равно полусумме абсолютных величин разностей между соответствующими индексами. Не то, чтобы считать таким способом было быстрее, чем с помощью диагоналей, но смотрится изящно.
Номинал в 7 баллов был назначен для ММ120 дабы не спугнуть участников :) На самом деле 7 баллов планировалось ставить тем участникам, которые разберутся с диаметром и заметят непостоянство радиуса для многоугольников с нечетным числом сторон. В итоге я почти угадал :)
При подведении итогов я столкнулся дилеммой. Чье решение лучше: того участника, который больше нашел больше других, но при этом кое-в чем ошибся; того, который не ошибался (реже ошибался), но при этом и обнаружил меньше локальных закономерностей? Если добавить сюда, что строгость обоснований тоже разнится, станет понятно, с какими трудностями я столкнулся. Так что, не обессудьте!
Ясно, что точку ставить рано. Получены (а тем более обоснованы) ответы не на все вопросы задачи. Кроме того, возникает целый ряд новых вопросов. В общем, есть что пообсуждать. Если же обсуждение (по не самой лучшей марафонской традиции) не завяжется, пеняйте на себя. Новые встречи с выпуклыми многоугольниками и их графами вам гарантированы! :)
Награды
За решение задачи ММ120 Сергей Половинкин получает 8 призовых баллов, Алексей Волошин и Анатолий Казмерчук - по 7 призовых баллов, а Николай Дерюгин - 4 призовых балла.
Эстетическая оценка задачи - 4.7 балла