

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ16
Конкурсная задача ММ16 (8 баллов)
Эта задача перекликается с задачей ММ15
Вновь рассматриваются перестановки множества {1,2,…n}.
Назовем перестановку правильной, если она не оставляет на месте ни одного элемента множества {1,2,…n}. Сколько существует правильных перестановок для n=20?
Решение
Рассмотрим количество правильных перестановок n-элементного множества R(n) для небольших значений n:
R(1) = 0
R(2) = 1
R(3) = 2
R(4) = 9
R(5) = 44
R(6) = 265.
Легко увидеть следующую рекуррентную формулу для r(n):
R(n) = nR(n-1) + (-1)n (1)
Однако доказать эту формулу не так просто. Поэтому мы применим несколько иной подход к вычислению R(n).
Введем в рассмотрение еще одну функцию - r(n,i), определяемую как количество перестановок n-элементного множества, переставляющих ровно i элементов.
Ясно, что r(n,i) = C(n,i)R(i).
Суммируя по всем i, получим: 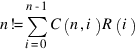 (2)
(2)
Отсюда 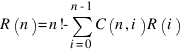
И мы нашли приемлемую формулу для R(n).
Применив ее к n=20, получим R(20) = 895014631192902121.
Обсуждение
Обращая формулу (2), можно получить следующее выражение для R(n):
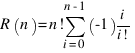 (3)
(3)
Подставляя выражения для R из (3), в формулу (1) не трудно убедиться в ее справедливости.
Видно, что с ростом n второй сомножитель в (3) стремится к 1/e. Оценивая хвост ряда, не участвующий в (3), можно показать, что R(n) есть n!/e, округленное до ближайшего целого.
перестановки, которые в условии ММ16 называются «правильными», обычно называют «беспорядками». Подробнее про них можно почитать в книжке: Р. Грэхем, Д. Кнут, О. Паташник «Конкретная математика».
Награды
За правильное решение (узнавание) этой задачи Борис Бух получает 8 призовых баллов.