

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
160
Конкурсная задача ММ160 (ТГ-5) (10 баллов)
На множестве натуральных чисел от 1 до 10460353203 структура графа G задается так:
вершины a и b смежны тогда и только тогда, когда множества цифр в g-ичной записи чисел a и b различны при любом натуральном g \ge 2.
Является ли G:
a) двудольным;
B) связным;
с) ациклическим?
d) Чему равна степень вершины 3?
e) Есть ли G вершины, степень которых больше чем 10000000000?
Решение
Положим n = 10460353203=321.
Обозначим U1={2k-1|k ∈ {1,2, …, 33}}, U2=V U1. Очевидно, что числа из U1 и только они записываются в двоичной системе с помощью одних единиц. Поэтому эти 33 вершины попарно не смежны. Вершины из U2 в двоичной записи имеют нули и единицы. Соответственно и эти вершины попарно не смежны. Таким образом, граф двудольный.
Не сложно найти в G изолированные вершины. Их имеет смысл искать среди чисел из U2, в троичную запись которых входят все троичные цифры. Такая вершина будет заведомо не смежна всем вершинам из U2 и большинству вершин из U1. Дело в том, что в троичную запись большинства вершин из U1 входят все троичные цифры. Исключение составляют вершины 1, 3, 7, 31, 255 и 32767. Однако вершина 1, очевидно, не смежна никакой вершине, кроме 2. Для того чтобы искомая вершина a была не смежна 3, достаточно взять число a, кратное 3 и большее 12. Тогда запись этого числа в системе счисления c основанием g = a-3 будет состоять из двух троек (*). Аналогично можно обеспечить отсутствие смежности вершинам 7, 31, 255 и 32767. Впрочем, поскольку подходящих вершин много, можно найти одну из них подбором. Легко проверяется, что наименьшей изолированной вершиной будет 87.
Ясно, что в силу двудольности в графе не может быть цикла, длина которого меньше 4. В то же время цикл длины 4 (в виду огромного числа таких циклов) найти легко. Такими циклами будут, например, (2,3,4,7) или (31,88,255,70);
Подсчитаем число вершин, не смежных 3.
Такими будут все, кратные 3, за исключением 6. В самом деле, в троичной записи множества цифр чисел 3, 9, и 12 совпадают. А начиная с 15, числа кратные 3 не смежны вершине 3 на основании рассуждения аналогичного (*). Таким образом, у нас уже есть 320-1 подходящих вершин.
Среди чисел, не кратных 3, отсутствие смежности вершины a вершине 3 может быть обусловлено одной из двух причин:
1) множество цифр в троичной записи a равно {0,1};
2) a \in U1.
Легко видеть, что число вершин, удовлетворяющих условию (1) равно 220-21. В самом деле, числа, не превосходящие n будем записывать упорядоченный набор из 21-й троичной цифры, возможно, с нулями старших разрядах (набор из одних нулей сопоставим числу 321). Тогда в каждой позиции можно поставить либо 0, либо 1. Но в младшем разряде должна быть 1, что обеспечит отсутствие кратности 3. Это дает 220. Остается заметить, что ровно 21 из этих чисел записывается с помощью одних единиц.
Вершина 2i-1 из U1 кратна 3 тогда и только тогда, когда i четно. Поэтому ровно 17 вершин из U1 не кратны 3. Но одна из них (31) учтена в предыдущем пункте.
Окончательно получаем: deg(3)=321-(320-1)-(220-21)-16=6972520232.
Покажем, что степень вершины 31 больше 10000000000. Для упрощения оценки пренебрежем возможными пересечениями множеств вершин не смежных 31.
Не смежными с вершиной 31 будут вершины кратные 31, начиная 312+62. Таких менее чем [{321/31].
Для дальнейших оценок заметим, что в системах с основаниями 2, 5 и 30 число 31 записывается одними единицами. Других вершин, имеющих подобную запись в нашем графе соответственно 32, 13 и 4.
В остальных системах с основаниями, меньшими 32, множества цифр в записи числа 31 двухэлементы. Пусть g - одно из таких оснований. Тогда количество чисел, не превосходящих n и записываемых теми же цифрами, что и 31, заведомо не превосходит 2k, где k - наименьшее натуральное такое, что gk>n.
Из приведенных соображений получаем оценку
deg(31)>[30/31*321]-(32+13+4+221+218+214+2*213+2*312+2*211+5*210+9*29+3*28+27)>10000000000
Ответ: Граф G:
двудолен;
не связен;
имеет циклы;
степень вершины 3 равна 6972520232;
в G есть вершины степень которых больше 10000000000.
Обсуждение
Вершина 31 не единственная вершина, степень которой превышает 10000000000. Рассуждениями, аналогичными приведенным, можно показать, что еще большую степень имеет вершина 255. «Третье место» занимает вершина 32767. Но ее степень уже меньше 10000000000 (подвело основание 7).
Ясно, что 87, далеко не единственная изолированная вершина. Таковыми будут, например, 375, 501, 885, 1407, 1527, 1533, 1917, 3573, 3927, 3933, 6015, 6135, 7551, 7677, 8031…
Остальные вершины образуют одну большую компоненту связности диаметра 4.
С подробным обоснованием вышеперечисленных и некоторых других свойств графа G можно познакомиться в :решении Олнга Полубасова.
Замечу, что по ходу решения Олег «изобрел велосипед». Его теорема 9 - это известная формула для подсчета числа сюръективных отображений (в нашем случае из m-элементного множества позиций в k-элементное множество цифр).
Внеся первое слагаемое под знак суммы, можно записать ее проще: 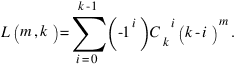 Или даже так: L(m,k)=k!S(m,k), где S(m,k) - соответствующее число Стирлинга второго рода.
Впрочем, «велосипед функционирует исправно». И это главное! К тому же, не мне судить Олега. В свое время, я «наступил на те же грабли» - вывел формулу для числа сюръекций и был очень доволен собой, пока не заглянул в книжку.
Или даже так: L(m,k)=k!S(m,k), где S(m,k) - соответствующее число Стирлинга второго рода.
Впрочем, «велосипед функционирует исправно». И это главное! К тому же, не мне судить Олега. В свое время, я «наступил на те же грабли» - вывел формулу для числа сюръекций и был очень доволен собой, пока не заглянул в книжку.
Число 321 в качестве количества вершин было выбрано по следующим соображениям:
1) оно достаточно велико, чтобы избежать исследования графа полным перебором;
2) чтобы легче вычислялась степень вершины 3;
3) чтобы проходила красивая оценка для максимума степеней вершин.
Отмечу, что второе соображение сработало лишь частично. Практически никто из участников (включая автора задачи) не вычислил степень вершины 3 с первого раза. Тем самым, подтвердилось предположение Алексея Волошина, что с первого раза такое не вычисляется ![]()
Если уйти от частного случая n=321, появится много новых интересных вопросов:
Будет ли граф иметь изолированные вершины при любых больших n?
Если «да», то какова асимптотика их количества по отношению к n?
Будет ли вершина 255 оставаться самой высоковалентной при любых больших n?
Если нет, то какие вершины ее «победят»?
Замечу, что вершина 87 остается изолированной при n ≤ 102000. Не исключаю. что так будет и при любых больших n. Но боюсь, что доказать эту гипотезу настолько трудно, что проще опровергнуть ![]()
Награды
За правильное решение и некоторое обобщение задачи ММ160 Олег Полубасов получает 12 призовых баллов. Алексей Волошин получает 10 призовых баллов, Сергей Половинкин, Виктор Филимоненков и Анатолий Казмерчук - по 9 призовых баллов а Николай Дерюгин - 7 призовых баллов.
Эстетическая оценка задачи - 4.8 балла.
Разбор задачи ММ160 подготовил Владимир Лецко