

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
MM166
Конкурсная задача ММ166 (3 балла)
Для каждого из натуральных чисел от 1 до 10000000000 находят знакочередующуюся сумму всех натуральных делителей, упорядоченных по возрастанию (делитель 1 берется со знаком минус). Сколько отрицательных и сколько нечетных чисел при этом получится?
Решение
Очевидно, что знакочередующаяся сумма, в которой каждое следующее слагаемое по абсолютной величине больше предыдущего, меняет знак при добавлении каждого следующего слагаемого. Чтобы итоговая сумма была отрицательной, необходимо и достаточно, чтобы число натуральных делителей исходного числа было нечетным. А это, в свою очередь, равносильно тому, что исходное число является полным квадратом. Поэтому имеется ровно 100000 чисел, для которых интересующая нас сумма отрицательна. Однако простой пример -1+7-49 = -43 = -1+2-4+8-16+32-64 (и пара свежих задач про «похожие числа») показывает, что разные квадраты могут давать одни и те же суммы. Но сто тысяч - это не десять миллиардов. Такое количество уже вполне посильно для компьютерного перебора. Такой перебор показывает, что 100000 квадратов дадут ровно 98506 сумм.
Очевидно, что четность знакочередующейся суммы натуральных делителей числа n равносильна четности σ(n), т. е. просто суммы натуральных делителей числа n.
Пусть 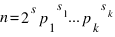 - каноническое разложение числа n. Нечетность интересующей нас суммы равносильна нечетности всех сомножителей в произведении
- каноническое разложение числа n. Нечетность интересующей нас суммы равносильна нечетности всех сомножителей в произведении 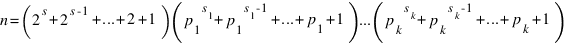 . Первый сомножитель нечетен всегда, а остальные - только при четности всех показателей si.
Поэтому интересующая нас сумма будет нечетной будет тогда и только тогда, когда n - квадрат (при четных s) или удвоенный квадрат (при нечетных s).
Количество сумм для первого случая уже посчитано. Остается проверить сколько сумм дают [√(1010)/2]=70710 удвоенных квадратов.
Их оказывается ровно 70709 (интересующие нас суммы совпадают только для чисел 2⋅7652 и 2⋅8352).
Итого, имеется 98506+70709=169215 нечетных сумм.
. Первый сомножитель нечетен всегда, а остальные - только при четности всех показателей si.
Поэтому интересующая нас сумма будет нечетной будет тогда и только тогда, когда n - квадрат (при четных s) или удвоенный квадрат (при нечетных s).
Количество сумм для первого случая уже посчитано. Остается проверить сколько сумм дают [√(1010)/2]=70710 удвоенных квадратов.
Их оказывается ровно 70709 (интересующие нас суммы совпадают только для чисел 2⋅7652 и 2⋅8352).
Итого, имеется 98506+70709=169215 нечетных сумм.
Обсуждение
Задача вновь оказалась коварной. Хотя, в отличие от ММ165, я никого «ловить» и «покупать» не собирался. Но, по-видимому, на уровне подсознания сделал это.
Я полагал, что условие сформулировано вполне однозначно, но… пятеро из шести человек, решавших ММ166, искали количества чисел, дающих отрицательные и нечетные суммы, а не количество таких сумм. Получается, когда я забываю упомянуть что-то в условии (см. разбор ММ164), это не мешает участникам включить телепатию и понять, что я имел в виду. А когда недомолвок нет… все гораздо сложнее ![]() Если исключить сговор (а я не сторонник теории мирового заговора), придется признать, нечеткость условия.
Поэтому я решил не считать ошибочными решения с ответами 100000 и 170710, а наоборот поощрить единственного участника, не утратившего «астральной связи» с ведущим.
Удивительно, что и у этого участника (Анатолия Казмерчука) ответ не совпал с моим. Почему это удивительно? Дело в том, что Анатолий прислал maple-код, с помощью которого считал свой ответ. Не найдя ошибок, я запустил программку Анатолия на исполнение и получил такой же ответ как… у меня. С учетом похожей ситуации с задачей ММ165 следует признать такую картину традицией
Если исключить сговор (а я не сторонник теории мирового заговора), придется признать, нечеткость условия.
Поэтому я решил не считать ошибочными решения с ответами 100000 и 170710, а наоборот поощрить единственного участника, не утратившего «астральной связи» с ведущим.
Удивительно, что и у этого участника (Анатолия Казмерчука) ответ не совпал с моим. Почему это удивительно? Дело в том, что Анатолий прислал maple-код, с помощью которого считал свой ответ. Не найдя ошибок, я запустил программку Анатолия на исполнение и получил такой же ответ как… у меня. С учетом похожей ситуации с задачей ММ165 следует признать такую картину традицией ![]()
Еще одной неожиданностью для меня стал тяжеловесный, громоздкий подсчет числа удвоенных квадратов, осуществленный (одним бы - ладно) половиной (!) участников.
Сначала я начинал знакочередующиеся суммы делителей с 1, но затем решил хоть чуть-чуть спрятаться от A071323 из OEIS.
Любопытно, что знакочередующиеся суммы для квадратов повторяются довольно часто, а для удвоенных квадратов нашелся всего один повтор.
Награды
За решение задачи ММ166 Анатолий Казмерчук получает 4 призовых балла, а Виктор Филимоненков, Олег Полубасов, Сергей Половинкин, Алексей Волошин и Николай Дерюгин по 3 призовых балла.
Эстетическая оценка 4.1 балла