

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ172
Конкурсная задача ММ172 (А-2) (5 баллов)
Доказать, что существует бесконечно много хитовых abc-троек, таких что c является степенью пятерки.
Примечание:
Тройка натуральных чисел a,b,c называется хитовой abc-тройкой, если a+b = c, GCD(a,b) = 1 и c > rad(abc).
Примечание к примечанию:
Пусть 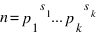 , тогда
, тогда 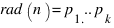
Решение
Построим требуемые хитовые тройки с помощью пифагоровых.
Положим a0=2, b0=1, an+1=|an2-bn2|, bn+1=2anbn.
Непосредственно проверяется что:
an и bn всегда взаимно просты;
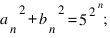
все тройки, начиная с n=2, хитовые;
Обсуждение
Достаточно легко получить и другие бесконечные множества хитовых троек, которых c является степенью пятерки:
(a=1, b=54k/sup>-1), c=5<sup>4k/sup>;
(a=1, b=5^<sup>6k/sup>-1), c=5<sup>6k/sup>;
несколько более общий случай - 1, 5<sup>p(p-1)-1, 5p(p-1), где p>5 - простое число.
Во всех этих примерах a (или, если угодно, b) равно единице. Составляя задачу, я планировал в формулировке условия отсечь такие тройки. Но, верный своей рассеянности, забыл. И заметил свою оплошность, лишь когда мне указал на нее Алексей Волошин (и то со второго раза). Однако к этому времени я уже получил решение, в котором a=1. После этого вносить изменения в условие было бы дурным тоном.
Ниже приведены решения Олега Полубасова и Анатолия Казмерчука, в которых a отлично от единицы. Решение Николая Дерюгина по сути повторяет решение Анатолия, но менее строго аргументировано.
Специально для Олега Полубасова отмечу, что так полюбившийся ему термин «хитовые тройки» придуман не мной.
Многие марафонцы отметили, что пятерка не является уникальным числом: присланные ими решения позволяют строить аналогичные множества хитовых троек и для степеней других чисел. Приведенное выше решение также допускает подобное обобщение. Например, положив a0=3, b0=2, можно получить бесконечно много хитовых троек, у которых c будет степенью числа 13.
Награды
За правильное решение задачи ММ172 Сергей Половинкин, Алексей Волошин, Виктор Филимоненков, Олег Полубасов, Анатолий Казмерчук, Кирилл Веденский и Алексей Извалов получают по 5 призовых баллов. Николай Дерюгин получает 4 призовых балла.
Эстетическая оценка задачи - 4.6 балла