| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ25
Конкурсная задача ММ25 (4 баллов)
Единичный квадрат перегнули по прямой, проходящей через его центр. Какова наибольшая возможная площадь получившейся фигуры?
Решение
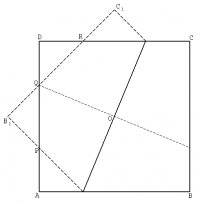
Пусть ABCD - исходный квадрат, а прямая MN (M лежит на AB ближе к A, N - на CD) проходит через центр квадрата, точку O. Пусть, далее, B1 и C1 - точки, симметричные соответственно точкам B и C относительно прямой MN, P - точка пересечения прямых AD и MB1, Q - точка пересечения прямых AD и B1C1 и R - точка пересечения прямых CD и B1C1.
Очевидно, что площадь фигуры, полученной перегибанием квадрата по MN, равна сумме половины площади квадрата и площадей треугольников PQB1 и RNC1.
Докажем, что четыре прямоугольных треугольника PMA, PQB1, RQD и RNC1 равны. Во-первых, очевидно подобие этих треугольников. Для доказательства их равенства докажем равенство соответствующих катетов. Пусть AM = a. Ясно, что C1N = CN = a. Пусть X - точка на BC такая, что BX = a. Тогда Q - образ X одновременно при центральной симметрии относительно O и осевой симметрии относительно MN. Поэтому DQ = B1Q = BX = a и равенство треугольников доказано.
MB1 = MB = 1-a. Но PB1 = PA. Поэтому MA+AP+MP = 1. Из всех прямоугольных треугольников с периметром 1 наибольшую площадь будет иметь тот, у которого будет наибольшим радиус вписанной окружности - r (площадь равна r/2). Ясно, что наибольшим r будет обладать равнобедренный треугольник. Значит, 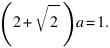 Отсюда
Отсюда 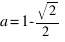 , а искомая площадь равна
, а искомая площадь равна 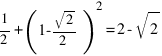 .
.
Обсуждение
Предлагая данную задачу, я не заметил изопериметричности возникающих треугольников. Поэтому мне не удавалось найти элементарного обоснования того интуитивно ясного факта, что максимум площади достигается, когда треугольники будут равнобедренными. Мое решение было таким:
Обозначим угол ABB1 через a. Тогда интересующая нас площадь будет выражаться формулой
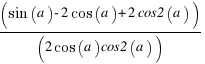
Исследуя эту функцию на экстремум получим, что максимум достигается при a = p/8, откуда следует равнобедренность возникающих прямоугольных треугольников.
Награды
За правильное (более изящное, чем авторское) решение задачи Андрей Бежан получает 5 призовых баллов.