

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ34
Конкурсная задача ММ34 (4 балла)
Последовательность задана рекуррентно:
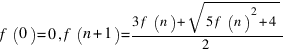
Доказать, что она целочисленная.
Решение
Уединяя корень и возводя обе части в квадрат, получим:
f(n+1)2 - 3f(n)f(n+1) + f(n)2 - 1 = 0
Подставив в это соотношение n-1 вместо n получим:
f(n-1)2 - 3f(n)f(n-1) + f(n)2 - 1 = 0
Таким образом, f(n+1) и f(n-1) являются корнями одного и того же квадратного уравнения (f(n+1) - больший из корней, поскольку последовательность, очевидно, возрастающая).
По формулам Виета имеем: f(n+1) = 3f(n) - f(n-1).
Поскольку f(0) и f(1) - целые, последнее соотношение гарантирует целочисленность всех членов последовательности.
Обсуждение
Отмечу, что наша последовательность представляет собой прореженный (через один) ряд Фибоначчи.
Разумеется. можно получить и другие аналогичные целочисленные последовательности, стартуя с соотношения
f(n+1) = kf(n) - f(n-1).
Можно отталкиваться и от соотношения
f(n+1)2 - kf(n)f(n+1) + f(n)2 - b = 0, подбирая k и b так, чтобы при целом f(0) и f(1) тоже было целым.
Так, при 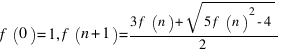 получим вторую половину ряда Фибоначчи.
получим вторую половину ряда Фибоначчи.
Задача ММ34 была опубликована в «Кванте» №1, 2008 в разделе «Конкурс имени А.П.Савина» под номером 19 (разбор в №4, 2008).
Награды
За правильное решение этой задачки Влад Франк, Мигель Митрофанов и Иван Козначеев получают по 4 призовых балла. Константин Владимиpов получает 2 призовых балла.