

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ35
Конкурсная задача ММ35 (5 баллов)
Васе и Пете задали задачку:
«В прямоугольном треугольнике с катетами a и b провели биссектрису прямого угла. В получившиеся при этом два треугольника вписали по окружности. Найти их радиусы.»
Васе и Пете были известны конкретные числовые значения a и b.
У Васи получились ответы 3 и 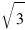 , а у Пети - 2 и
, а у Пети - 2 и 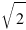 .
Кто из них ошибся?
.
Кто из них ошибся?
Решение
Зафиксируем меньший катет BC треугольника ABC, взяв его равным 1, а длину большего катета AB обозначим через x.
Тогда отношение площади треугольника ACD к площади треугольника BCD будет равно x (поскольку биссектриса делит противолежащую сторону в отношении прилежащих, а высота, опущенная из C, у них общая).
Обозначим через 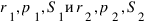 радиус вписанной окружности, полупериметр и площадь треугольников BCD и ACD соответственно.
радиус вписанной окружности, полупериметр и площадь треугольников BCD и ACD соответственно.
Тогда 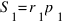 и
и 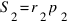 , откуда
, откуда
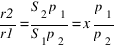 (1)
(1)
Легко видеть, что 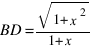 ,
,
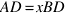 и
и 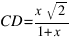 .
.
Подставляя эти значения в выражение (1), получим
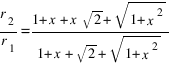 (2)
(2)
Не трудно проверить, что с ростом x от 1 до бесконечности (2) монотонно возрастает от 1 до 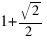 .
Учитывая, что отношение радиусов
.
Учитывая, что отношение радиусов 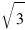 , которое получилось у Васи, не входит в указанный диапазон, делаем вывод, что он ошибся.
, которое получилось у Васи, не входит в указанный диапазон, делаем вывод, что он ошибся.
Обсуждение
Разумеется, ответ Пети тоже не обязан быть верным.
Более того, учитывая, что его ответ получается при
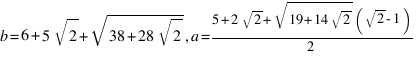 , можно с уверенностью предположить, что Петя тоже ошибся (или что учитель, задавший мальчикам эту задачу, - садист)
, можно с уверенностью предположить, что Петя тоже ошибся (или что учитель, задавший мальчикам эту задачу, - садист) ![]()
Награды
За решение этой задачи Иван Козначеев получает 7 призовых баллов (два балла добавлены за нахождение значений a и b, при которых получается Петин ответ), Мигель Митрофанов - 5 призовых баллов, а Влад Франк - 3 призовых балла.