

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ37
Конкурсная задача ММ37 (13 баллов)
Монетный двор Дурляндии чеканит монеты трех достоинств: 6, 10 и 15 дурок.
1) Некоторые суммы (в целое число дурок) в принципе не могут быть набраны дурляндскими монетами. Какова максимальная из них? (2 балла);
2) Доказать, что два дурляндца, в кошельках которых достаточно монет подходящих достоинств, всегда смогут осуществить взаиморасчет с точностью до одной дурки (1 балл);
3) Обобщить 1-й пункт задачи на случай монет достоинством в ab, ac и bc дурок, где a, b и c - попарно взаимно простые натуральные числа (5 баллов);
4) Обобщить 3-й пункт задачи на случай монет достоинством в
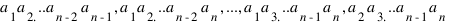 дурок, где
дурок, где 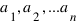 - попарно взаимно простые числа. (5 баллов).
- попарно взаимно простые числа. (5 баллов).
Решение
1) Непосредственно проверяется, что сумма в 29 дурок не набираема дурляндскими монетами. В то же время:
30 = 15 + 15;
31 = 15 + 10 + 6;
32 = 10 + 10 + 6 + 6;
33 = 15 + 6 + 6 + 6;
34 = 10 + 6 + 6 + 6 + 6;
35 = 15 + 10 + 10.
Любая последующая сумма может быть получена добавлением некоторого числа монет достоинством в 6 дурок к одной из перечисленных сумм.
2) Первый дурляндец может заплатить второму 1 дурку, отдав ему по монете в 10 и 6 дурок, и получив сдачу монетой в 15 дурок. Повторяя этот процесс, он может заплатить партнеру любое целое число дурок.
Прежде чем, приступать к разбору 3-го и 4-го пунктов, докажем одну лемму.
Обозначим максимальную целочисленную сумму, не набираемую дурками достоинствами 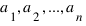 через
через 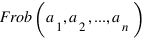 .
.
ЛЕММА. Для взаимно прстых a и b Frob(a,b) = ab - a - b.
Пусть для определенности a < b.
Попробуем выяснить чему должен равняться коэффициент при b в представлении ab - a - b = sa + tb с целыми неотрицательными s и t.
Для этого будем, стартуя с ab - a - b, вычитать b, пока не получим число, кратное a. Числа
ab - a - b,
ab - a - 2b,
ab - a - 3b,
………
ab - a - ab
образуют полную систему вычетов по модулю a. Поэтому среди них ровно одно кратно a. Ясно, что это последнее число. Но оно отрицательно. Поэтому ab - a - b не представимо в требуемом виде. Остается показать, что число ab - a - b + k (k - любое натуральное) обладает необходимым представлением.
Числа
k + ab - a - b,
k + ab - a - 2b,
k + ab - a - 3b,
………
k + ab - a - ab
тоже образуют полную систему вычетов по модулю a. Значит, среди них тоже ровно одно число кратное a. При k < a это число не может быть последним, а все остальные числа неотрицательны. Если же k не меньше a, то все числа системы неотрицательны. Поэтому в любом случае мы придем к требуемому представлению.
3. Пусть числа a, b, c попарно взаимно просты. Покажем, что
Frob(ab,ac,bc) = 2abc - ab - ac - bc.
Зададимся вопросом, сколько дурок достоинством bc должно участвовать в представлении суммы S = 2abc - ab - ac - bc, если такое представление существует.
Для этого перепишем S в виде a(bc - b - c) + bc(a - 1). Числа
a(bc - b - c) + bc(a - 1),
a(bc - b - c) + bc(a - 2),
a(bc - b - c) + bc(a - 3),
………………
a(bc - b - c) + bc,
a(bc - b - c)
образуют полную систему вычетов по модулю a. Монетами достоинствами ab и ac дурок, очевидно может быть набрана лишь сумма, кратная a.
Поэтому коэффициент при bc в искомом разложении должен быть равен a - 1. И нам остается набрать сумму a(bc - b - c) дурками достоинств ab и ac. Ясно, что это равносильно набору суммы bc - b - c дурками достоинств b и c. Но последнее невозможно в силу доказанной леммы.
Для доказательства того, что всякая сумма, бОльшая S, имеет требуемое представление вновь рассмотрим полную систему вычетов по модулю a:
a(bc - b - c) + bc(a - 1) + k,
a(bc - b - c) + bc(a - 2) + k,
a(bc - b - c) + bc(a - 3) + k,
………………
a(bc - b - c) + bc + k,
a(bc - b - c) + k.
Ровно одно из чисел системы кратно a. Пусть это a(bc - b - c) + sbc + k. Тогда sbc + k делится на a. Обозначим частное этого деления через t. Согласно лемме, число bc - b - c + t представляется в виде линейной комбинации чисел b и c с целыми неотрицательными коэффициентами. Домножая это представление на a и добавляя bc(a - 1 - s), получим требуемое представление для 2abc - ab - ac - bc +k.
4. 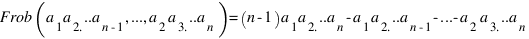 .
.
Доказательство можно провести по индукции. В качестве базы индукции годится утверждение леммы. Индуктивный переход делается примерно также, как получение формулы для Frob(ab,ac,bc) из формулы для Frob(a,b).
Обсуждение
Вопросы задачи MM37 представляют собой частные случаи известной задачи размена (coin problem). В общем виде эта задача формулируется так:
Пусть числа натуральные 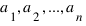 - взаимно просты (в совокупности). Ясно, что в этом случае любое натуральное число, начиная с некоторого, может быть представлено в виде линейной комбинации чисел
- взаимно просты (в совокупности). Ясно, что в этом случае любое натуральное число, начиная с некоторого, может быть представлено в виде линейной комбинации чисел 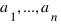 с целыми неотрицательными коэффициентами. Требуется найти максимамальное целое число, не представимое в виде такой комбинации. Это число (которое, на самом деле, есть функция от
с целыми неотрицательными коэффициентами. Требуется найти максимамальное целое число, не представимое в виде такой комбинации. Это число (которое, на самом деле, есть функция от 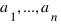 ) называется числом Фробениуса.
) называется числом Фробениуса.
При n = 2 для чисел Фробениуса имеется простая формула Frob(a,b) = ab - a - b.
Для n = 3 ситуация значительно сложнее. Формула (скорее, даже не формула, а быстрый алгоритм) для Frob(a,b,c) была найдена лишь в 1978 году.
Для бОльших значений n общая формула неизвестна. Более того, AFAIK, доказано что при n>3 задача отыскания числа Фробениуса является в общем случае NP-сложной.
4-й пункт задачи являет собой вполне пробиваемый частный случай задачи размена для произвольного n. Любопытно, что этот пункт одновременно является обобщением общего случая для n = 2.
Награды
За правильное решение этой задачи Мигель Митрофанов и Иван Козначеев получают по 13 призовых баллов. За верное решение первого пункта Влад Франк получает 2 призовых балла.