

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ51
Конкурсная задача ММ4 (3 балла)
1) Какое наибольшее (при данном n) число можно получить, расставляя скобки в выражении 1:2:3:…:n? (1 балл)
2) Верно ли, что для любого положительного рационального числа a существуют такое n и такой способ расстановки скобок, что значение выражения 1:2:3:…:n станет равным а? (2 балла)
Решение
1) При любой расстановке скобок 1 окажется в числителе, а 2 - в знаменателе. Остальные числа можно загнать в числитель, расставив скобки так:
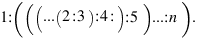
Поэтому наибольшим значением выражения (при n > 1) будет n!/4.
2) Нет, не верно.
Например, нельзя получить число 2.
При n = 2 двойка попадает в знаменатель. Для того чтобы она оказалась в числителе, надо взять n не меньше 4. Но тогда либо в числитель, либо в знаменатель выражения попадет тройка. Для ее нейтрализации придется увеличивать n, по крайней мере, до 6. При этом в числитель или знаменатель выражения попадет пятерка…
Поскольку (постулат Бертрана) между числами p и 2p лежит хотя бы одно простое число закончить процесс нейтрализации «лишних» простых множителей не удастся.
Oбсуждение
Легко видеть, что каждое следующее n, начиная с 3, назависимо от распределения предыдущих, можно отправить как в числитель, так и в знаменатель. Отсюда следует, что оценкой сверху для количества различных чисел, получаемых расставовкой скобок в выражении 1:2:3:…:n, является число 2n-2.
Эта оценка точна вплоть до n = 7. В общем случае точный ответ на этот вопрос мне неизвестен.
Награды
За правильное решение этой задачки Иван Козначеев, Алексей Ковальский, Виктор Филимоненков и Влад Франк получают по три призовых балла. Дмитрий Милосердов получает 4 призовых балла (один балл добавлен за наиболее оперативную реакцию на мой прокол при первоначальном формулировании задачи).
Эстетическая оценка задачи - 2 балла