

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Эта задача в еще большей степени чем задача 45 навеяна известной
задачей Иосифа Флавия (Josephus problem).
Ее решение учитывается дважды:
В Большом Маpафоне и в мини-конкуpсе арифметических задач.
Конкурсная задача №75 (А-3) (8 баллов)
Для каждого натурального q, большего 1, опрелелим функцию натурального
аргумента Jq(n) следующим образом:
Расставим натуральные числа от 1 до n по кругу. Пропускаем 1 и вычеркиваем
числа 2,… q. Пропускаем число q+1 и вычеркиваем следующие q-1 чисел.
И так далее. До тех пор, пока не останется всего одно число.
Оно-то и будет значением Jq(n).
1. Для каждого q описать все n, для которых Jq(n) = n.
2. Найти явную формулу для J3(n).
Решение
Приведу решение Анатолия Казмерчука.
Ясно, что 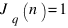 при n = 1,…, q.
при n = 1,…, q.
Далее, пусть n>q. После вычёркивания чисел с 2 по q остаётся n-q+1 чисел,
причём теперь на первом месте стоит число q+1, на 2-ом - q+2, и т. д.
На месте с номером n-q стоит число n. И, наконец, на месте с номером n-q+1
стоит число 1. Поэтому, справедлива реккурентная формула
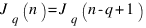 , если Jq(n-q+1) < n-q+1 и
, если Jq(n-q+1) < n-q+1 и
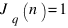 , если Jq(n-q+1) = n-q+1
, если Jq(n-q+1) = n-q+1
Из формулы видно, что, если 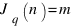 , и n>m, то
, и n>m, то 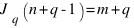 .
Поэтому, для r = 1,…, q-1 имеем:
.
Поэтому, для r = 1,…, q-1 имеем:
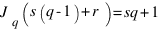 , если sq < s(q-1)+r, то есть при s < r,
а при s = r имеем
, если sq < s(q-1)+r, то есть при s < r,
а при s = r имеем 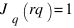 .
Далее,
.
Далее, 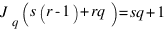 , если sq<s(q-1)+rq, то есть при s < rq,
а при s = rq имеем
, если sq<s(q-1)+rq, то есть при s < rq,
а при s = rq имеем 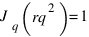 .
.
И т.д.
в общем случае при k = 0,1,2,…
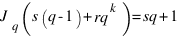 , если sq<s(q-1)+rqk, то есть при
s < rqk, а при s = rqk имеем
, если sq<s(q-1)+rqk, то есть при
s < rqk, а при s = rqk имеем 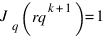 .
.
Выведем теперь общую формулу для 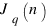 при q > 1.
Представим число n в виде n = s(q-1)+rqk,
где r = 1,…q-1, k = 0,1,2,.., s = 0,…, rqk-1.
Число r даёт тот же остаток при делении на q-1, что и n.
при q > 1.
Представим число n в виде n = s(q-1)+rqk,
где r = 1,…q-1, k = 0,1,2,.., s = 0,…, rqk-1.
Число r даёт тот же остаток при делении на q-1, что и n.
Поэтому r = (n-1) mod (q-1) + 1, затем, ![k = [log_q(n/r)] k = [log_q(n/r)]](http://www-old.fizmat.vspu.ru/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_980.5_5db26aba10dd91969841e0aecd1a0c70.png) ,
,
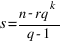 .
После последовательных подстановок получаем явную формулу для
.
После последовательных подстановок получаем явную формулу для 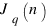 :
:
![J_q(n) = q/{q-1}(n-((n-1)mod(q-1)+1)q^{[log_q(n/{(n-1)mod(q-1)+1})]}) + 1 J_q(n) = q/{q-1}(n-((n-1)mod(q-1)+1)q^{[log_q(n/{(n-1)mod(q-1)+1})]}) + 1](http://www-old.fizmat.vspu.ru/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_949.5_79354cc9ecd0026a5953baf03d5fd376.png) (1)
(1)
Перейдём теперь к поставленным в задаче вопросам.
Из рассмотрений видно, что
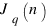 = n на каждом шаге при s = rqk-1, то есть при
n = rqk-q+1, где r = 1,..,q-1, k = 1,2,.. Отметим, что эти числа
в системе счисления с основанием q оканчиваются единицей, а все остальные
цифры, за исключением, возможно, первой - q-1.
= n на каждом шаге при s = rqk-1, то есть при
n = rqk-q+1, где r = 1,..,q-1, k = 1,2,.. Отметим, что эти числа
в системе счисления с основанием q оканчиваются единицей, а все остальные
цифры, за исключением, возможно, первой - q-1.
Формула при n = 3 вытекает из общей формулы (1):
![J_3(n) = 3/2(n-((n-1)mod 2 +1)3^{[log_3(n/{(n-1)mod 2 +1})]}) + 1 J_3(n) = 3/2(n-((n-1)mod 2 +1)3^{[log_3(n/{(n-1)mod 2 +1})]}) + 1](http://www-old.fizmat.vspu.ru/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_949.5_654231c21d00554304b4934d4127c445.png)
Обсуждение
В классическом варианте задачи Иосифа Флавия наоборот вычеркивается (а не оставляется) каждое q-е число из n, расставленных по кругу. В этом случае явную формулу удается найти лишь для q = 2. Для бОльших q известен лишь достаточно быстрый алгоритм, позволяющий находить номер последнего невычеркнутого числа за время O(q*log(n)), да и то в случае, когда q значительно меньше n. Подробности можно найти, в статье известного марафонца: М.А. Алексеев <Задача Иосифа Флавия>. Империя Математики, 2 (2001), стр. 22-28.
Задача неожиданно для меня удостоилась наивысшей оценки от участников Марафона.
Мне очень приятна такая оценка, но…
Полагаю, что этот успех во многом обусловлен тем, что часть марафонцев забывает
давать задачам эстетическую оценку. Рискуя ухудшить собственные показатели, я,
тем не менее, призываю участников давать задачам свою оценку.
Награды
За верное решение задачи и обобщение второго пункта на любое q Анатолий Казмерчук и Олег Полубасов получают по 9 призовых баллов. За правильное решение здачи Константин Кноп и Виктор Филимоненков получают по 8 призовых баллов. Влад Франк, решивший только первый пункт, получает 3 призовых балла.
Эстетическая оценка - 5 баллов