

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
№84
Задача 84 являлась мини-конкурсом.
Дабы не ввести участников Марафона в заблуждение, сразу уточню,
что префикс «мини» не означает легкости этой задачи.
Просто конкурс состоял всего из одной задачи.
Конкурсная задача №84 (9 баллов)
Имеется двадцать мешков, наполненных одинаковыми с виду монетами.
В первом мешке каждая монета имеет вес 20 грамм, во втором - 21,
в третьем 22, … в двадцатом - 39. Мешки перепутаны и расставлены
в случайном порядке.
С помощью одного взвешивания на стрелочных весах (показывающих точный вес
в граммах) выяснить веса монет в каждом из мешков.
При этом во взвешивании желательно использовать по возможности меньше монет.
Примечания:
1. Мешки содержат, а весы вмещают (не теряя точности) столько монет, сколько потребуется для решения задачи.
2. 20 мешков взяты для того, чтобы исключить решение задачи компьютерным перебором. Впрочем, если кто-либо из участников сможет преодолеть эту трудность (и убедить ведущего в корректности компьютерного решения), оно будет принято ;)
3. 9 баллов будут присуждаться тем участникам, в решениях которых будет использовано столько же монет, сколько в решении ведущего (разумеется, достаточность указанного количества монет должна быть строго обоснована). За решения более (менее) оптимальные, чем решение ведущего, будет начисляться больше (меньше) девяти баллов.
4. Известное мне решение заведомо не оптимально.
Решение
Не нарушая общности, можно считать, что веса монет: 0, 1, 2,…, 19.
Возьмем из первого (не мешка с самыми легкими монетами, а первого в некой
нумерации) с1, из второго - с2, …, из 20-го - с20 монет.
Для каждой перестановки (a1, a2, …, a20) чисел 0, 1, …, 19 образуем
сумму s = с1*a1 + c2*a2 + … + c20*a20.
Очевидно, что набор с = (с1, с2, с3,…, с20) будет решением тогда и
только тогда, когда все 20! таких сумм будут попарно различны.
Очевидно, что решением будет набор (0, 1, 20, 202, …, 2018).
В самом деле, s будет 19-значным (если знаков 18, то припишем ведущий ноль)
числом в 20-ричной системе счисления без повторов цифр. Каждая цифра укажет
вес монет в соответствующем мешке (отсутствующая в s цифра укажет вес монет в
мешке, из которого не брали ни одной монеты).
Приведенное выше решение обладает следующим свойством:
Пусть s = с1*a1 + c2*a2 + …ck*ak + ck+1*ak+1 + … + c20*a20,
t = с1*b1 + c2*b2 + …ck*bk + ck+1*bk+1 + … + c20*b20 и
ak < bk, а ak+1 = bk+1, ak+2 = bk+2, …, a20 = b20
Тогда s < t. Такие решения будем называть простыми.
Наша цель - построить минимальный набор, являющийся простым решением.
Ясно, что можно взять c1 = 0 и c2 = 1.
Пусть мы уже нашли c1, c2, …, ck-1.
Возьмем bk = ak + 1 и ak+1 = bk+1, …, a20 = b20.
t - s = ck + (bk-1 - ak-1)*ck-1 + … + (b1 - a1)*c1.
Поэтому в качестве ck годится
max[(ak-1 - bk-1)*ck-1 + … + (a1 - b1)*c1)] + 1,
где подстановки (ai) и (bi) таковы, что ak+1 = bk+1, …, a20 = b20.
При нечетных k требуемый максимум достигается при подстановках
a = (1, 2, …, (k-3)/2, (k-1)/2, 20-(k-3)/2, 20-(k-1)/2, …, 20, 20-(k-1)/2, ak+1, …, a20),
b = (20, 19, …, 20-(k-5)/2, 20-(k-1)/2, (k-1)/2, (k-3)/2,…,1, 20-(k-3)/2, ak+1, …, a20).
Для конкретных значений k эти подстановки выглядят не так страшно, как в
общем виде. Например, при k = 9
a = (1, 2, 3, 4, 17, 18, 19, 20, 16, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15),
b = (20, 19, 18, 16, 4, 3, 2, 1, 17, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15).
При четных k соответствующие подстановки:
a = (1, 2, …, k/2-1, x+1, 20-k/2, 20-(k-2)/2,…, 20, x, ak+1, …, a20),
b = (20, 19, …, 20-k/2, x, k/2-1, k/2-2, …, 1, x+1, ak+1, …, a20),
где x - любое из диапазона k/2…18-k/2.
Объединяя эти случаи, получим:
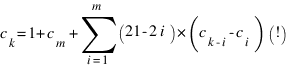 , где m = [k/2].
, где m = [k/2].
К с1 и С2 добавим c3, c4, …, c20, найденные по формулам (!):
с1 = 0
с2 = 1
с3 = 20
с4 = 382
с5 = 7583
с6 = 150575
с7 = 2995270
с8 = 59583716
с9 = 1185362498
с10 = 23581699460
с11 = 469137721669
с12 = 9333093638159
с13 = 185673936682779
с14 = 3693824593531841
с15 = 73485489860293368
с16 = 1461931145788096982
с17 = 29083873284686161512
с18 = 578598853768938868016
с19 = 11510730716885865621286
с20 = 228996170271688893675650
Просуммировав Сi получим простое решение, использующее 241116123021589624090767 монет, что на 34824929609989323277654 монет меньше, чем 1 + 20 + … + 2018 монет.
Найденное решение является лучшимм в классе простых решений, но, конечно
же не самым оптимальным.
Уже для 5 мешков решение, построенное по формулам (!) (естественно с заменой
21 на 6), дает набор (0, 1, 5, 22, 98) с суммой 126, в то время как простой
перебор показывает, что оптимальным решением будет набор (0, 2, 5, 21, 91)
с суммой 119.
Олег Полубасов предложил способ позволяющий получать решения оптимальнее
простых.
Рекурсивное описание и обоснование этого метода являются результатом работы
некой компьютерой программы.
Поскольку итоговый документ получается весьма объемным, а используемые в нем
обозначения отличны от принятых здесь, он прилагается в отдельном сообщении:marathon:pbas_84.txt.
Здесь же я приведу лишь один набор сi, полученный этим методом:
с1 = 0
с2 = 9
с3 = 20
с4 = 381
с5 = 7260
с6 = 144276
с7 = 2864893
с8 = 56994127
с9 = 1133762542
с10 = 22555232416
с11 = 448715673503
с12 = 8926815545228
с13 = 177591358923194
с14 = 3533028620029147
с15 = 70286590786211882
с16 = 1398291777251722095
с17 = 27817822320525771015
с18 = 553411849636947006320
с19 = 11009656751280514450481
с20 = 219027731084943424487352
Sum = 230620089806568708826141, что существенно меньше суммы ci, полученных
по формулам (!).
В то же время ясно, что и это решение не оптимально.
Обсуждение
С условием этой задачи (для разных количеств мешков) я сталкивался не раз.
Однако ни разу не встречал решения лучше, чем 0 + 1 + 20 + … + 2018.
Набор с суммой 241116123021589624090767 - это тот ответ, получив который
я решил поместить данную задачу в марафон. Именно за его получение и
обоснование в третьем пункте примечания обещано 9 баллов.
Разумеется, формулы (!) и метод, предложенный Олегом Полубасовым,
тривиально обобщаются на любое число мешков.
Например, формулы (!) для n мешков выглядят так:
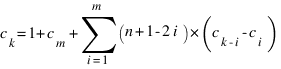 , где m = [k/2]
, где m = [k/2]
Награды
Победителем конкурса, который являла собой задача 84, стал Олег Полубасов. С чем я Олега и поздравляю!
За правильное и более оптимальное, чем у ведущего, решение задачи 84 Олег Полубасов получает 15 призовых баллов. За решение, совпадающее с решением ведущего Анатолий Казмерчук получает 9 призовых баллов. За очевидное, но не слишком оптимальные решение Галина Крюкова и Николай Дерюгин получают по 3 призовых балла. За столь же очевидные, но еще менее оптимальное решение Влад Франк получает 2 призовых балла.
Эстетическая оценка задачи - 5 баллов