

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
159
Конкурсная задача ММ159 (6 баллов)
Для натурального числа n, большего 1, обозначим через qu(n) отношение суммы количеств единиц во всех записях числа n в системах счисления с натуральными основаниями, большими 1, к самому числу n. Найти наибольшее и наименьшее значение qu(n) и предел qu(n) при n, стремящимся к бесконечности. Конечны ли множества чисел, для которых qu(n): меньше 1; больше 1; равно 1?
Решение
Пусть g - основание системы счисления. При g>n число n будет записываться одной цифрой, отличной от 1. Поэтому суммарное число единиц во всех записях n конечно.
Очевидно, что при n/2 < g ≤ n n будет двухзначным, причем первая цифра будет 1. При g = n-1 единицами будут обе цифры в записи n. Поэтому при n > 2 qu(n) > 1/2. В то же время, qu(2) = 1/2. Значит, наименьшее значение qu(n) равно 1/2.
Для 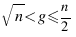 n по-прежнему двузначно, но первая цифра отлична от единицы, а вторая не может быть единицей часто. Суммарное количество всех цифр (и, тем более, всех единиц) во всех записях n с основаниями
n по-прежнему двузначно, но первая цифра отлична от единицы, а вторая не может быть единицей часто. Суммарное количество всех цифр (и, тем более, всех единиц) во всех записях n с основаниями 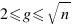 с ростом n растет медленнее, чем n/2.
с ростом n растет медленнее, чем n/2.
Из этих соображений следует простой план решения задачи: показать, что 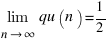 ; найти какое-то n0, что для всех n > n0 qu(n) < 1, и перебрать значения qu(n) для n, не превосходящих nsub<>0</sub>.
Наименьшим количеством перебираемых n удалось обойтись Олегу Полубасову. Познакомиться с его решением можно :здесь.
; найти какое-то n0, что для всех n > n0 qu(n) < 1, и перебрать значения qu(n) для n, не превосходящих nsub<>0</sub>.
Наименьшим количеством перебираемых n удалось обойтись Олегу Полубасову. Познакомиться с его решением можно :здесь.
Ответ:
наименьшее значение qu(2) = 1/2;
наибольшее значение qu(7) = 9/7;
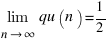 ;
;
при n ∈ {5, 7, 9, 11, 13, 31} значение qu(n) больше 1;
при n ∈ {3, 4, 6, 10, 15, 21} значение qu(n) равно 1;
при остальных n значение qu(n) меньше 1.
Обсуждение
Я ожидал, что кто-либо из участников по традиции обобщит задачу ММ159. Тем более, что естественные обобщения напрашиваются. Однако, не дождался. Придется самому.
Обозначим через quc(n) отношение суммарного количества цифр «c» в записях натурального числа n (n>c) во всех системах счисления с натуральными основаниями g (g>1) к самому числу n.
Легко видеть, что при c> 1 quc(n) = 0, для всех n\in {c+1, c+2,…, 2c}.
Не сложно доказывается и то, что 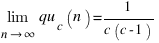 . Причем при достаточно больших n значение quc(n) всегда больше этого предела.
. Причем при достаточно больших n значение quc(n) всегда больше этого предела.
Особняком стоит случай c=0. 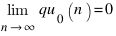 . Однако стремление к нулю очень неравномерное, с резкими всплесками на числах, имеющих много мелких делителей.
. Однако стремление к нулю очень неравномерное, с резкими всплесками на числах, имеющих много мелких делителей.
Более содержательным представляется вопрос о наибольших значениях quc(n) при различных c. Обозначим через mqu© наибольшее значение функции quc(n). Ниже приведена таблица значений mqu© для небольших c (во втором столбце указаны n, при которых достигается наибольшее значение; в третьем - суммарное количество цифр «c» в записях этого n).
| c | n | Σ | mq© |
|---|---|---|---|
| 0 | 4 | 3 | 3/4 |
| 1 | 7 | 9 | 9/7 |
| 2 | 26 | 14 | 7/13 |
| 3 | 15 | 5 | 1/3 |
| 4 | 28 | 6 | 3/14 |
| 5 | 35 | 6 | 6/35 |
| 6 | 54 | 7 | 7/54 |
| 7 | 79 | 9 | 9/79 |
| 8 | 80 | 8 | 1/10 |
| 9 | 69 | 6 | 2/23 |
| 10 | 130 | 10 | 1/13 |
| 11 | 71 | 5 | 5/71 |
| 12 | 192 | 11 | 11/192 |
| 13 | 73 | 4 | 4/73 |
| 14 | 74 | 4 | 2/37 |
| 15 | 63 | 3 | 1/21 |
Полагаю второй и третий столбцы этой таблицы - достойные кандидаты в OEIS.
Гипотеза 1. При c>0 mqu© строго монотонна.
Гипотеза 2. При каждом c существует единственное значение n, при котором достигается наибольшее значение quc(n).
Гипотеза 3. Значения n, для которых quc(n) достигает mqu© уникальны (не повторятся при других c).
Для больших c mqu© существуют целые участки, где mqu© ведет себя закономерно. Вот пример такого поведения:
| c | n | Σ |
|---|---|---|
| 54 | 474 | 7 |
| 55 | 475 | 7 |
| 56 | 476 | 7 |
| 57 | 477 | 7 |
| 58 | 478 | 7 |
| 59 | 479 | 7 |
По-видимому, с ростом c такие участки будут встречаться все чаще и иметь все большую длину.
Награды
За правильное (и наименее зависящее от компьютерного перебора) решение задачи ММ159 Олег Полубасов получает 7 призовых баллов. За верное решение Виктор Филимоненков, Алексей Волошин, Сергей Половинкин и Анатолий Казмерчук получают по 6 призовых баллов.
Эстетическая оценка задачи - балла
Разбор задачи ММ159 подготовил Владимир Лецко