| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ20
Конкурсная задача ММ20 (6 баллов)
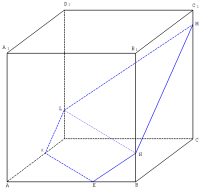
Куб ABCDA1B1C1D1 склеен из единичных кубиков. Сечения EKLMN и OPRST, параллельные BD, имеют площади 50 и 100 соответственно. Найти объем куба.
Решение
Обозначим ребро куба a.
Будем рассматривать сечения, у которых одна из вершин (пусть это будет E) лежит на AB (остальные пятиугольные сечения, параллельные BD не отличаются от этих). Тогда остальные вершины сечения лежат на ребрах AD, DD1, CC1, BB1. Пусть это будут соответственно точки K, L, M и N.
Ясно, что рассматриваемые сечения вполне определяются положением точек E и M, и площадь их будет тем меньше, чем ближе точка M к С, а точка E к B. При этом площадь ограничена снизу площадью треугольника BCD равной a2/2. Отсюда a<10. (1)
Для того, чтобы сделать площадь сечения наибольшей, точку M, очевидно, надо совместить c С1. Однако зависимость площади от положения точки E, не столь прозрачна (с одной стороны, устремляя ее к A, мы 'удлиняем' сечение, а с другой - сужаем его нижнюю часть).
Обозначим, AE = x и найдем площадь как функцию от x (при этом временно положим a=1, чтоб не путалось под ногами). Обозначим 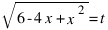 . Тогда площадь треугольника LMN будет равна
. Тогда площадь треугольника LMN будет равна 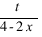 , а площадь трапеции EKLN -
, а площадь трапеции EKLN - 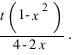 Суммируя эти выражения находим площадь сечения:
Суммируя эти выражения находим площадь сечения:
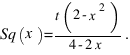
Производная функции Sq(x) будет равна 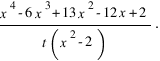
Знаменатель не обращается в 0 на интересующем нас промежутке (0; 1), а числитель раскладывается на два множителя 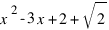 и
и 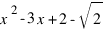 . Корни первого комплексны, а второй имеет два вещественных корня, из которых один,
. Корни первого комплексны, а второй имеет два вещественных корня, из которых один,
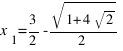 , принадлежит (0, 1).
, принадлежит (0, 1).
Легко убедиться, что при x = x1 Sq(x) имеет максимум. Вспоминая про a, находим что максимум площади сечения a2Sq(x1) будет превышать 100, начиная с a=9.
Соотнеся последний вывод с (1) окончательно получаем a = 9 и V = 729.
Награды
За правильное решение этой задачи Владимир Трушков получает 6 призовых баллов. За правильно, но неполное решение Дмитрий Максимов получает 4 призовых балла.