

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ59
Конкурсная задача ММ59 (8 баллов)
Сколько существует гомоморфизмов из кольца классов вычетов по модулю m в кольцо классов вычетов по модулю n?
Решение
Напомню, что гомоморфизмом кольца К в кольцо К' называется отображение f:K → K', при котором f(x + y) = f(x) + f(y) (1) и f(x*y) = f(x)*f(y) (2), для любых x и y из К.
Пусть f(1) = a (здесь и в дальнейшем предполагается, что элементы, к которым применяется гомоморфизм f, являются классами вычетов по модулю m, а их образы - классами вычетов по модулю n). Тогда a*a = f(1)*f(1) = f(1) = a, т.е. образ единицы первого кольца должен быть идемпотентом во втором.
Пусть 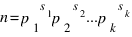 . Тогда в кольце Zn имеется ровно 2k идемпотентов. В самом деле, сравнение x(x-1) == 0 имеет ровно два решения (0 и 1) для каждого модуля
. Тогда в кольце Zn имеется ровно 2k идемпотентов. В самом деле, сравнение x(x-1) == 0 имеет ровно два решения (0 и 1) для каждого модуля 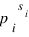 , откуда на основании китайской теоремы об остатках получаем 2k решений по модулю m.
, откуда на основании китайской теоремы об остатках получаем 2k решений по модулю m.
Взяв в качестве f(1) идемпотент a кольца Zn, мы можем доопределить f для остальных элементов кольца Zn, используя соотношение (1). Однако, очевидно, что при этом должно выполняться условие m кратно n/(a,n), поскольку в противном случае число элементов образа кольца Zm не будет делителем количества элементов самого Zm.
Таким образом, нас устроят только идемпотенты, кратные всем 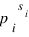 , для которых si превосходит показатель pi в разложении m. Таких идемпотентов будет 2t, где t - количество простых делителей в разложении n, показатели которых не превосходят их показателей в разложении m.
, для которых si превосходит показатель pi в разложении m. Таких идемпотентов будет 2t, где t - количество простых делителей в разложении n, показатели которых не превосходят их показателей в разложении m.
Легко проверяется, что отображение 1 в каждый из таких идемпотентов единственным образом достраивается до отображения Zm в Zn с использованием (1) и при этом (2) будет выполняться автоматически.
Окончательно получаем: число гомоморфизмов из Zm в Zn равно 2t, где t - количество простых делителей в разложении n, показатели которых не превосходят их показателей в разложении m.
Награды
За правильное решение этой задачи Владислав Франк и Виктор Филимоненков получают по 8 призовых баллов.
Эстетическая оценка задачи - 3 балла