| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ183
Легкая задача с очевидным неочевидным обобщением
Конкурсная задача ММ183 (3 балла)
Про пять чисел a,b,c,d,e известно, что a<b<c<d<e. Попарные суммы этих чисел выписали в порядке неубывания. Найти число вариантов расположения сумм в этом списке в зависимости от конкретных значений исходных чисел.
Решение
Привожу решения:
Андрея Халявина (кратко, обоснованно, но без обобщений);
Олега Полубасова (решение и модификации);
Анатолия Казмерчука (модификация без решения) ![]()
Обсуждение
Остановимся на обобщении ММ183 и ее близких аналогов.
Хотя Олег Полубасов и утверждает, что ему неизвестно, какие обобщения имел в виду ведущий. полагаю он немного лукавит, поскольку под номером 1 в его списке стоит «правильная» версия.
Тем более, что остальные «обобщения» Олега - это не обобщения а вариации на тему (что, разумеется, тоже приветствуется).
Меня же в первую очередь заинтересовал вопрос о наличии общей формулы, наподобие той, что есть для последовательности A003121 в OEIS.
Эта последовательность вообще сыграла злую шутку с некоторыми участниками. Значения a(2), a(3), a(4), a(5) совпадают с ответами на аналоги ММ183 при соответствующих значениях n. А среди многочисленных интерпретаций есть и такая: количество способов заполнения треугольной таблицы числами 1,2,…,n(n-1)/2, так чтобы в каждой строке и в каждом столбце числа возрастали.
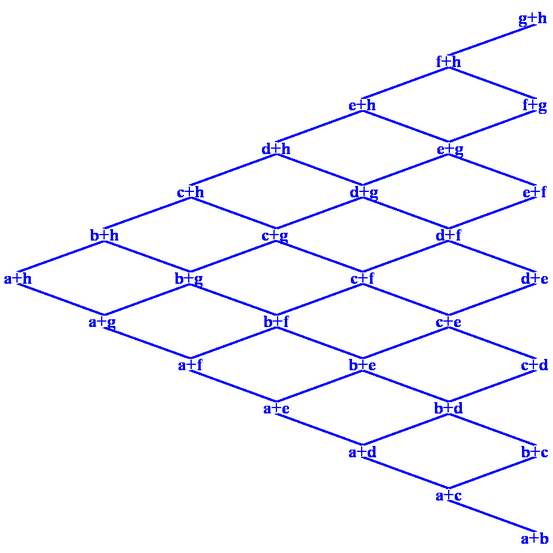
А количество наших сумм - тоже треугольное число. Более того, решетка (ч.у.м., в котором у любой пары элементов есть точная верхняя и точная нижняя грань) имеет именно треугольный вид.
(На рисунке представлена решетка сумм для восьми чисел. В примерах рассматривается случай шести чисел, но картинку я рисовал раньше, когда оптимистично замахивался на любые n):
В общем, создается впечатление, что общая задача решена. Остается указать биекцию между числовыми треугольниками и возможными упорядочиваниями сумм и добавить в OEIS еще одно описание A003121. И такая биекция находится! Проиллюстрирую ее на примере следующего треугольника
| b | 1 | |||
|---|---|---|---|---|
| c | 2 | 4 | ||
| d | 3 | 6 | 8 | |
| e | 5 | 7 | 9 | 10 |
| a | b | c | d |
Выпышем попарные суммы элементов a<b<c<d<e в следующем порядке: на i-е место поставим сумму индексов столбца и строки, на пересечении которых стоит число i. Для нашего треугольника получим a+b, a+c, a+d, b+c, a+e, b+d, b+e, c+d, c+e, d+e. Легко убедиться, что при n⇐5 указанное соответствие задает биекцию, между всеми треугольниками и всеми вариантами упорядочивания сумм.
К моменту, когда мне прислали первое решение с выходом на A003121, я уже давно имел ответ о числе упорядочиваний сумм для n=6 и не сомневался в нем.
Этот ответ был 168. А шестой член A003121 равен 286. Поэтому я решил, что совпадение начальных членов A003121 и ответов к ММ183 для малых n - случайность. И успокоился. Но ненадолго. В тот же день пришло еще одно решение с ответом 286 для n=6.
Уверенность в правильности моего ответа пошатнулась и я кинулся перепроверять свое решение. И, как мне показалось, разгадал загадку.
Дело в том, что первоначально условие ММ183 выглядело немного по-другому. В нем говорилось, что все попарные суммы различны. Но при публикации я убрал эту оговорку, рассуждая примерно так:
для n=5 решение не изменится, зато ответ будет попроще, а обобщения… а обобщения все равно можно рассмотреть и в предположении попарного различия сумм и без него.
Ответ 168 соответствовал ситуации, когда все суммы различны. Ясно, что если допустить равенство сумм число упорядочиваний по неубыванию возрастет.
Например, при различии всех сумм порядок a+d, a+e, b+c, b+d, a+f, b+e, b+f, c+d, c+e, c+f, d+e невозможен.
В самом деле, из неравенств a+e<b+c и b+d<a+f следует, что d+e<c+f.
Но такое упорядочивание легко достигается, если допустить равные суммы. Например, при a=1,b=5,c=9,d=12,e=13,f=16.
Итак, все ясно! Добавляем в OEIS новую последовательность, в описание A003121 добавляем новую интерпретацию и ссылку на новую последовательность.
Но на всякий случай я решил пересчитать возможные упорядочивания сумм, среди которых могут быть равные.
И их оказалось 244. Т.е. меньше, чем способов заполнить треугольник числами от 1 до 15.
Приведу пример «лишнего» треугольника:
| b | 1 | ||||
|---|---|---|---|---|---|
| c | 2 | 5 | |||
| d | 3 | 6 | 10 | ||
| e | 4 | 7 | 11 | 13 | |
| f | 8 | 9 | 12 | 14 | 15 |
| a | b | c | d | e |
Описанный выше способ ставит ему в соответствие такое «упорядочивание» множества сумм:
a+b,a+c,a+d,a+e,b+c,b+d,b+e,a+f,b+f,c+d,c+e,c+f,d+e,d+f,e+f.
Но из a+e ≤ b+c и b+e ≤ a+f следует 2e ≤ c+f. Но c+f ≤ d+e<2e и мы пришли к противоречию.
Что ж? Тем лучше. Добавим в OEIS две новых последовательности! А общая формула?.. Будем думать.
В прилагаемом файле приведены 286 расположений сумм, соответствующих 286 способам заполнения треугольника числами 1,2,…, 15. Они разбиты на три группы: 168 расположений соответствующих упорядочиваниям попарно различных сумм; 76 реализуемых только при наличии равных сумм; 42 нереализуемых.
И еще об одной сложной задаче. Эту задачу задал мне своей версией решения Анатолий Казмерчук. Задача - во сколько баллов оценить его решение? Готов убедительно обосновать любое количество баллов от 0 до 7 включительно! Не верите?! Тогда обосную крайние случаи: 0. Исходная задача вообще не решена, решавшаяся вместо нее решена неверно - итого 0 баллов. … 7. Исходная задача правильно решена в первом же пункте измененной задачи, гораздо более сложной, чем исходная. Измененная задача решена практически верно: правильно выбраны случаи; верно найдены ответы для каждого случая; верно найдены пересечения всех случаев. И лишь собирая все верно найденное воедино Анатолий допустил оплошность, за которую можно и не снижать баллы. Итак, можно считать, что решена и исходная и более сложная задача (в точности та, за которую начислены дополнительные баллы Олегу Полубасову). Значит, и оценка должна быть такой же!
В итоге я остановился на 5 баллах. А сколько поставили бы вы?
Награды
За правильное решение и обобщение ММ183 Олег Полубасов получает 7 призовых баллов, Сергей Половинкин - 5 призовых баллов, Антон Никонов - 4 призоых балла. За правильное решение задачи ММ183 Андрей Халявин, Виктор Филимоненков, и Дмитрий Пашуткин получают по 3 призовых балла. За верные наблюдения (не приведшие, однако, к правильному решению) Николай Дерюгин получает один призовой балл. За практически правильное решение гораздо более сложного аналога ММ183 Анатолий Казмерчук получает 5 призовых баллов.
Эстетическая оценка задачи 4.6 балла