

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ214
Конкурсная задача ММ214 (4 балла)
1. Все грани многогранника - n-угольники. При каких n это возможно?
2. При каком наименьшем числе граней существует многогранник, все грани которого пятиугольны?
Решение
В качестве образца типового решения приведу то, которое прислал Виктор Филимоненков. Решения с обобщениями традиционно представлены Олегом Полубасовым и Анатолием Казмерчуком.
Обсуждение
Для решения ММ214 практически все участники в той или иной форме перевывели часть, так называемой, теоремы Эберхарда:
Для любого многогранника справедливо соотношение 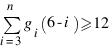 , где gi - количество i-угольных граней, а n - наибольшее число сторон в гранях. Причем это неравенство обращается в равенство тогда и только тогда, когда многогранник является простым (степень каждой вершины равна 3).
, где gi - количество i-угольных граней, а n - наибольшее число сторон в гранях. Причем это неравенство обращается в равенство тогда и только тогда, когда многогранник является простым (степень каждой вершины равна 3).
Кроме того в теореме Эберхарда утверждается, для любого набора gi, удовлетворяющего соотношению 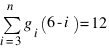 , при подходящем значении g6 найдется соответствующий многогранник.
, при подходящем значении g6 найдется соответствующий многогранник.
Поскольку большинство марафонцев получили требуемые соотношения еще при решении предыдущих задач конкурса, ответы на ММ214 получились совсем короткими.
Олег Полубасов и Анатолий Казмерчук заинтересовались естественным вопросом о возможных количествах граней многогранников, все грани которых имеют поровну сторон. При n=3 ответ на этот вопрос тривиален. При n=4 ответ был получен при обобщении ММ211. Поэтому интересен лишь случай n=5.
Вопрос о максимальной возможной степени вершин рассматриваемых многогранников показался мне менее несколько «притянутым за уши» к MM214.
Награды
За правильное решение задачи ММ214 и получение ответа на ряд смежных вопросов Анатолий Казмерчук получает 7 призовых баллов, а Олег Полубасов - 6 призовых баллов. За правильное решение ММ214 Василий Дзюбенко, Игорь Ханов, Владислав Франк, Владимир Чубанов, Виктор Филимоненков, Владимир Дорофеев и Дмитрий Пашуткин получают 4 призовых балла.
Эстетическая оценка задачи - 4.2 балла