| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
ММ219
Конкурсная задача ММ219 (8 баллов)
Какое наибольшее количество диагоналей может иметь одиннадцатигранник?
Решение
Привожу решения Олега Полубасова, Анатолия Казмерчука и Владислава Франка.
Обсуждение
По мере продвижения к финишу конкурса задачи традиционно усложняются. Не удивительно, что часть марафонцев сошли с дистанции, а другие держатся из последних сил. Но есть и те, у кого открылось второе дыхание. Посмотрим, у кого хватит сил на финишный рывок.
Интересно, что Олег Полубасов и Анатолий Казмерчук, обобщая задачу, передоказали теорему Грюнбаума-Моцкина
В упоминавшейся ранее книжжке Бранко Грюнбаума есть расширенный вариант этой теоремы.
Пусть (g3, g4, g5, g6) - вектор, характеризующий количества треугольных, четытеругольных, пятиугольных и шестиугольных граней простого (степень каждой вершины равна 3) многогранника, и других граней у него нет, т.е. по теореме Эберхарда 3g3+2g4+g5=12. Тогда:
векторы 0, 0, 12, g6 и 0, 6, 0, g6 реализуемы тогда и только тогда, когда g6≠1;
вектор 4, 0, 0, g6 реализуем тогда и только тогда, когда g6 четно и отлично от 2;
вектор 3, 1, 1, g6 реализуем тогда и только тогда, тогда g6 нечетно и больше 1.
Предлагая данную задачу, я уже знал ответ на вопрос о наибольшем возможном числе диагоналей многогранника с произвольным фиксированным количеством граней. Но, в отличие от Анатолия и Олега я не предоказывал теорему Грюнбаума_Моцкина, а нашел ее в сети.
Вот как выглядит центральный фрагмент авторского решения MM219 «методом чайника» в свете этой теоремы:
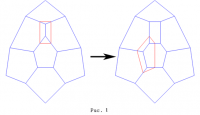
Предположим, что существует многогранник с вектором граней (0, 1, 10, 0). Фрагмент соответствующего графа приведен в левой части рис. 1.
Отсечением от него ребра, ровно одна вершина которого принадлежит четырехугольной грани, получим многогранник с вектором (0,1,10,1). У полученного многогранника отсечем шестигранник, как показано в правой части рис 1. Получим многогранник с вектором граней (0,0,12,1). Но по теореме Грюнбаума-Моцкина такого многогранника не существует. Значит, не существует и исходного многогранника. Остается привести пример многогранника с вектором (0,2,8,1),имеющего 73 диагонали.
Награды
За решение и обобщение ММ219 Олег Полубасов и Анатолий Казмерчук получают по 12 призовых баллов.
За решение ММ219 участникам начислены следующие призовые баллы:
Владислав Франк - 8;
Владимир Чубанов и Виктор Филимоненков- по 6.
Эстетическая оценка задачи - 4.8 балла