| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Математический марафон
Завершен 23-й конкурс в рамках Математического марафона
В упорной борьбе в Анатолием Казмерчуком победу вырвал Олег Полубасов.
В не менее напряженной борьбе на 3-е место Валентина Колыбасова опередила Виктора Филимоненкова.
Мои поздравления лауреатам!
Стать участником марафона может любой желающий. Некоторые задачи вполне доступны школьникам. Для решения других требуются знания, выходящие за рамки школьного курса. Одни задачи могут показаться вам интересными, а другие - не очень. На вкус и на цвет…
Но если любите поломать голову над нестандартными задачами, участвуйте, не стесняйтесь.
Жду от вас комментариев марафонских задач, а также пожеланий Марафону. Эта обратная связь позволит сделать Марафон интереснее для вас.
Не забывайте, пожалуйста, присылать вместе с Вашими решениями свои эстетические оценки задач по пятибалльной шкале.
Ведущий Марафона — Vladimir letsko
Текущие задачи
Появятся в 2018 году.
Разбор задач
Терминология ММ228-230
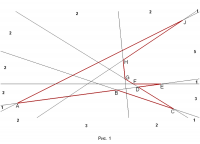
Несколько (не менее трех) прямых на плоскости называются прямыми общего положения, если любые 3 их них высекают треугольник. На рисунке 1 представлены 7 прямых общего положения.
Внешним контуром конфигурации n прямых общего положения назовем многоугольник, высекаемый данными прямыми. На рисунке 1 это красный девятиугольник ABCDEFGHJ.
Внешним циклом конфигурации назовем список количеств вершин внешних областей конфигурации, перечисленных в порядке обхода этих областей (направление и начало обхода не важны). Внешний цикл конфигурации, представленной на рисунке 1: (1, 2, 3, 3, 1, 3, 1, 5, 1, 2, 2, 2, 2, 2).
Выпуклыми вершинами внешнего контура назовем вершины, в которых углы меньше развернутого. На рисунке 1 выпуклыми вершинами являются A, C, E, J.
Обратными вершинами назовем вершины внешнего контура, углы при которых больше развернутого. На рисунке 1 это вершины B, D, F, G, H.
Элементарными отрезками назовем отрезки, концы которых являются соседним точками пересечения одной из прямых конфигурации с другими прямыми. Отрезок CD на рисунке 1 элементарен, а отрезок BC – нет.
Элементарными многоугольниками назовем многоугольники, стороны которых являются элементарными отрезками (одна сторона – один отрезок). Например, треугольник DEF на рисунке 1 элементарен, а треугольник BCD – нет.
Впадиной назовем участок внешнего контура между двумя соседними выпуклыми вершинами, содержащий хотя бы одну обратную вершину. Конфигурация, изображенная на рисунке 1 имеет 3 впадины ABC, CDE и EFGHJ.
Вектором граней конфигурации назовем упорядоченный набор из n-2 чисел (где n – количество прямых), первое из которых равно количеству элементарных треугольников, второе – количеству элементарных четырехугольников и т. д. Вектор граней конфигурации, представленной на рисунке 1 – [6, 8, 1, 0, 0].
ММ230
Конкурсная зхадача ММ230 (15 баллов)
Может ли вектор граней конфигурации нескольких прямых общего положения начинаться с чисел 157, 5250, 52?
Решение
Традиционно привожу решения Анатолия Казмерчука и Олега Полубасова.
Обсуждение
При составлении ММ230 я не избежал соблазна облегчить жизнь ведущему (при одновременном усложнении жизни конкурсантов). Как правило, изобретая задачу для Марафона, я колдую над ней, как минимум, не меньше, чем те, кто будет ее решать. С ММ230 картина иная. Я затратил на ее составление минут пятнадцать, при этом отдавая себе отчет (см. разбалловку) сколь тяжко будет конкурсантам. Я рассмотрел конфигурацию из n-1 = 2k-1 (k>2) прямых, являющихся сторонами правильного многоугольника. Ясно что, вектор грани конфигурации - (n-1,(n-1)(n-6)/2,0,… ,0,1). Осталось добавить к конфигурации n-ную прямую так, чтобы все точки пересечения остальных прямых лежали по одну сторону от этой прямой. Теперь возьмем какое-нибудь большое k (например 53), и пыточная камера для конкурсантов готова.
Выбраться из этой камеры удалось лишь двоим участникам. Не знаю как у вас, а у меня не было сомнений, что эти-то справятся. Жаль, что к ним никто не присоединился. Но подкоп в нужном направлении вели, по крайней мере, еще двое.
В решении Олега Полубасова меня восхитило то, с каким изяществом он описал все возможные векторы граней, начинающиеся с указанной тройки.
В целом же, после решения ММ228-230 круг нерешенных задач, связанных с конфигурациями прямых общего положения, скорее расширился, чем наоборот.
Награды
За решение (продвижение в сторону решения, решение и исследование) задачи ММ230 участники Марафона получают следующие призовые баллы: Олег Полубасов - 20; Анатолий Казмерчук - 17; Виктор Филимоненков - 5; Валентина Колыбасова - 4.
Эстетическая оценка задачи - 5 баллов
ММ229
Конкурсная задача ММ229 (7 баллов)
Петя нарисовал на доске несколько прямых общего положения так, что все попарные точки пересечения прямых попали на чертеж.
Вася выписал себе в тетрадь внешний цикл возникшей конфигурации: (1, 4, 3, 1, 4, 1, 2, 2, 3, 2, 3, 1, 2, 3, 1, 2, 4, 2, 1, 3).
После этого Петя стер рисунок. Сможет ли Вася восстановить:
1) количество прямых;
2) количество элементарных многоугольников:
3) количество выпуклых вершин;
4) количество элементарных отрезков, ограничивающих внешний контур;
5) количество сторон выпуклой оболочки внешнего контура;
6) суммарное число сторон элементарных многоугольников;
7) количество обратных вершин;
8) количество впадин;
9) количество сторон внешнего контура?
Примечание: Вася – умный.
ММ228
Конкурсная задача ММ228 (4 балла)
Какое наименьшее число элементарных четырехугольников может быть в конфигурации из семи прямых общего положения?
ММ227
Конкурсная зхадача ММ227 (7 баллов)
Пусть 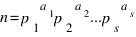 - каноническое разложение n. Обозначим через sopf(n) число
- каноническое разложение n. Обозначим через sopf(n) число 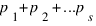 .
.
Назовем натуральное число k слабым, если уравнение x = k*sopf(x) неразрешимо в натуральных числах, и сильным в противном случае.
Доказать, что сильных чисел бесконечно много.
Найти наименьшее слабое число.
Доказать, что слабых чисел бесконечно много.
ММ226
Конкурсная зхадача ММ226 (5 баллов)
Назовем натуральное число n счастливым, если оно является точной седьмой степенью, а седьмой (при упорядочении по возрастанию) натуральный делитель n равен количеству натуральных делителей n. А есть ли, вообще, счастье в жизни? В смысле, существуют ли счастливые числа?
ММ225
Конкурсная задача ММ225 (6 баллов)
Найти все значения параметра a, при которых уравнение (2a+3)x2 + xa + 3a - 1 = 0 имеет два целых корня.
ММ224
Конкурсная задача ММ224 (6 баллов)
В задаче, которую задали на дом Пете и Васе, требовалось найти площади треугольников, на которые разбивается исходный треугольник ABC трисектрисами, проведенными из вершины C. При сверке ответов у Пети и Васи совпали значения двух площадей: 2 и 4. Третья площадь у Пети оказалась равной 10, а у Васи - 20. Найти угол С, если известно, что один из учеников получил за домашнее задание пятерку.
ММ223
Конкурсная задача ММ223 (6 баллов)
Рассмотрим две задачки.
1. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
2. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую попавшуюся из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
Какое из условий выгоднее для жуликоватого Васи?
Примечание: Был ли журнал электронным – не важно. Но важно, что колы не ставим: разрешается использовать только оценки 2, 3, 4, 5
ММ222
Конкурсная задача ММ222 (6 баллов)
На доске написано 10 попарно различных натуральных чисел. После того как 5 из этих чисел разделили на 5, а другие 5 умножили на 5 возникли 10 попарно различных натуральных чисел, отличных от исходных. При этом сумма новых чисел оказалась в 3 раза больше суммы исходных. Пусть n - наименьшее возможное значение наибольшего из исходных чисел, для которых возможна описанная ситуация. Сколько существует различных наборов исходных чисел с наибольшим числом n+1?
ММ221
Конкурсная задача ММ221 (4 балла)
Сколько решений в натуральных числах имеет уравнение 3x4 + 2y3 = 37z ?