

| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Это старая версия документа.
Содержание
ММ60
Конкурсная задача ММ60 (12 баллов)
Триша Тройкин, Петя Пятаков и Сёма Семак пытаются сконструировать собственный генератор псевдослучайных чисел. Для этого они взяли натуральные числа a и m (одни и те же у всех троих) и выстраивают последовательность по правилу:
xn+1 = xna (mod m).
Начав с некоторого x11, Триша посчитал x2, x3 и x4. Но x4 оказалось равно x1. Тогда он взял другое (не встречавшееся ранее) число в качестве x1. Но последовательность опять зациклилась на третьем шаге. Треья попытка привела Тришу к тому же результату.
Петя совершил пять попыток подобрать x1. Но всякий раз получал новые циклы длины 5. Наиболее упорным оказался Сёма. Он совершил семь попыток. И получил семь циклов длины 7.
При каком наименьшем m могла возникнуть такая ситуация?
ММ59
Конкурсная задача ММ59 (8 баллов)
Сколько существует гомоморфизмов из кольца классов вычетов по модулю m в кольцо классов вычетов по модулю n?
ММ58
Конкурсная задача ММ58 (8 баллов)
Обозначим через T(n) количество треугольников периметра n с целочисленными длинами сторон.
1) Конечно ли множество таких n, которые делят T(n)?
2) Конечно ли, множество таких n, при которых T(n) является полным квадратом?
3) Какие n встречаются чаще: те, при которых T(n) кратно 173, или те, при которых T(n) кратно 211?
ММ57
Конкурсная задача ММ57 (10 баллов)
Назовем многоугольник ординарным, если он выпуклый и никакие 3 его диагонали не пересекаются в одной точке внутри многоугольника. Пусть n - число сторон ординарного многоугольника.
1) На сколько частей разбивают диагонали ординарный многоугольник?
2) Верно ли, что при фиксированном n среди частей, на которые разбивается диагоналями ординарный многоугольник всегда одно и тоже число треугольников?
3) При каком минимальном n в разбиении ординарного многоугольника может получиться восьмиугольник?
4) Существует ли ординарный многоугольник, в разбиении которого получается больше пятиугольников, чем треугольников?
5) При каких n существуют разбиения ординарного многоугольника, содержащие только треугольники и четырехугольники?
ММ56
Конкурсная задача ММ56 (12 баллов)
Назовем трехпарным число, допускающее представление в виде суммы трех взаимно простых натуральных слагаемых, любые два из которых не взаимно просты. Конечно ли множество натуральных чисел, не являющихся трехпарными?
ММ55
Конкурсная задача ММ55 (7 баллов)
Через точку внутри тетраэдра провели 4 плоскости, параллельные граням. На сколько частей разобьется тетраэдр? (1 балл) Какой наименьший объем может иметь тетраэдр, если объемы частей попарно различны и целочисленны? (6 баллов).
ММ54
Конкурсная задача ММ54 (3 балла)
Доказать, что максимум площадей четырехугольников со сторонами a, b, c, d не зависит от порядка следования сторон.
ММ53
Конкурсная задача ММ53 (8 баллов)
Найти самое маленькое число, допускающее представление в виде суммы шести слагаемых, обладающее следующими свойствами:
1) каждое слагаемое является натуральным числом;
2) любые два слагаемых не взаимно просты;
3) любые три слагаемых взаимно просты;
4) сумма любых четырех слагаемых кратна 4;
5) сумма любых пяти слагаемых кратна 5.
ММ52
Конкурсная задача ММ52 (11 баллов)
Конечно ли множество натуpальных чисел m таких, что количество обpатимых элементов в кольце классов вычетов по модулю m pавно количеству квадpатов в том же кольце?
ММ51
Конкурсная задача ММ4 (3 балла)
1) Какое наибольшее (при данном n) число можно получить, расставляя скобки в выражении 1:2:3:…:n? (1 балл)
2) Верно ли, что для любого положительного рационального числа a существуют такое n и такой способ расстановки скобок, что значение выражения 1:2:3:…:n станет равным а? (2 балла)
ММ48
Конкурсная задача ММ48 (7 баллов)
Игоговую таблицу однокругового шахматного турнира будем называть «строгой», если никакие два участника не имеют поровну очков. Турнир с строгой таблицей также будем называть «строгим».
1) Гросмейстер Грустин Попалов выиграл в строгом турнире больше партий, чем каждый из других участников. На каком месте мог он оказаться в итоге, если в турнире участвовало n шахматистов? (2 балла)
2) Гроссмейстер Любомир Миролюбоевич шесть лет подряд играл в однокруговых рождественских турнирах в городе Зейк-ан-Вее. Каждый год он завершал все свои партии вничью, но год от года занимал все более высокое место. В каждом турнире было n участников и все они были строгие. При каком наименьшем n возможна такая ситуация? (2 балла)
3) Обозначим через d(n) количество мест, которые может занять Миролюбов, сыграв вничью, все партии строгого турнира при n участниках. Найти явное выражение для d(n). (3 балла)
ММ47
Конкурсная задача ММ47 (4 балла)
В разностороннем треугольнике ABC провели биссектрису AD. При этом оказалось, что длины всех сторон треугольников ABD и ACD целочисленны. При каком наименьшем периметре треугольника ABC возможна такая ситуация?
ММ45-46
Конкурсная задача ММ45-46 (30 баллов)
Функция f(n) задается так: Натуральные числа от 1 до n расставлены по кругу. Начинаем отмечать числа 1, 2, 4, 7, 11, 16 и т.д. Значением f(n) будет то число, которое первым будет отмечено повторно.
45.1) Доказать, что существует бесконечно много n, для которых f(n) = 500501. (5 баллов)
46.1) Найти явную формулу для f(3k). (4 балла)
46.2) Описать все такие n, для которых f(n) определяется на n+1-вом шаге, (т. е. все числа будут отмечены по разу, прежде чем какое-то будет отмечено повторно). Найти явное выражение f(n) для таких n. (4 балла)
46.3) Доказать, что на множестве нечетных простых чисел f(n) инъективна (т.е. f(p) не может равняться f(q), если p и q - различные нечетные простые числа). (7 баллов)
45.2) Верно ли, что для любого натурального m найдется n такое, что f(n) = m?
45.3) Верно ли, что существует бесконечно много таких n, для которых f(n) = n?
Решение
Числа 1, 2, 4, 7, 11, 16, естественным образом возникающие в этой задаче, я буду называть «посттреугольными» (поскольку каждое из них следует за соответствующим треугольным числом). Общая формула посттреугольных чисел - (k+1)k/2 + 1.
45.1.
Число 500501 является посттреугольным.
Докажем, что все посттреугольные числа встречаются в последовательности f(n) бесконечное число раз.
Пусть m - посттреугольное число. Тогда при n = t - m, где t - посттреугольное число, большее (m2 - m + 2)/2, f(n) будет равно m.
В самом деле, m (как и любое посттреугольное число, меньшее n) будет отмечено на первом круге. Оно же будет первым отмечено на втором круге.
Прежде чем рассматривать остальные пункты, докажем, что если m (равное f(n)) первый раз отмечается на k-том круге, повторно оно будет отмечено уже на следующем, k+1-вом круге.
Приведу доказательство этого факта, предложенное Андреем Винокуровым.
Пусть f(n) отмечается первый раз на i+1-вом шаге и на k-том круге, а второй раз - на j+1-вом шаге и на t-том круге.
Тогда f(n) = i(i+1)/2 + 1 - (k-1)n = j(j+1)/2 + 1 - (t-1)n.
Отсюда (j-i)(j+j+1) = 2(t-k)n. (1)
Надо доказать, что t-k = 1.
Соотношение (1) показывает, что 2(t-k)n = ab, где a и b - натуральные числа различной четности, и что пара натуральных чисел (j,i) является решением системы {x-y = a, x+y+1 = b}.
Очевидно, что эта система разрешима в натуральных числах всякий раз, когда b больше a и натуральные числа a и b имеют разную четность.
Допустим, что t-k > 1. Тогда у t-k имеется простой делитель p. Тогда 2(t-k)n/p = ab/p. Значит, на p делится, по крайней мере, одно из чисел a, b. Поделим его на p и обозначим через a' меньшее из получившихся чисел (a' может оказаться равным a/p, a или b/p), а через b' - большее (соответственно b' будет равно одному из чисел b, b/p или a). Отметим, что a' и b' по-прежнему будут разной четности (оба они не могут стать нечетными из-за множителя 2 в (1)).
Значит, система {x-y = a', x+y+1 = b'} разрешима в натуральных числах. Пусть (j',i') - ее решение. Тогда j' = (a'+b'-1)/2 < (a+b-1)/2 = j. Следовательно, значение f(n) определится раньше, чем на j-том шаге, что противоречит выбору j.
Теперь понятно, что значение f(n) определяется так:
Пусть 2n = ab - представление числа 2n в виде двух сомножителей разной четности такое, что a меньше b и разность b-a минимальна (Андрей Винокуров предложил называть такое представление «определяющим разбиением»).
Тогда f(n) = (x2 + x)/2 mod n + 1, где x = (a+b-1)/2 (тот же результат получится и при x = (b-a-1)/2 ).
46.1
Пусть n = 32k.
Тогда определяющее разбиение - 2n = ab, где a = 3k, b = 2*3k и f(n) = 1). Начиная с p = 13, ситуация будет несколько сложнее, т.к. значение f(pk) перестанет определяться для нечетных k уже на втором круге.
Однако для четных степеней нечетных простых чисел существует (найденная Олегом Полубасовым) простая формула f(n) = (n+7)/8.
Маша Никулина высказала гипотезу, что f(n) сюръективна уже на множестве простых n. К сожалению (для пункта 45.2), это не так. Наименьшее число, не представимое в виде f(n) ни при каком простом n - 7. А вообще таких чисел довольно много. В частности, значениями f(n) для простых нечетных n не могут быть посттреугольные числа, бОльшие 11 (еще одна несложная задачка про f(n)).
45.2
Я думаю, что ответ на вопрос этого пункта положителен. Однако доказать гипотезу о сюръективности f(n) пока не удалось ни мне, ни кому-либо из участников марафона.
Косвенным подтверждением справедливости гипотезы может служить тот факт, что для каждого конкретного m, как правило, без труда удается найти прообраз. Так, для чисел из первой тысячи я (пока) не смог найти прообраз только для m = 917.
Вот перечень чисел из первой тысячи, для которых известные мне наименьшие прообразы превышают миллиард:
209 = f(161 803 409 657);
224 = f(2 234 954 282);
588 = f(10 540 433 474 488);
705 = f(868 109 938 408);
770 = f(1 029 467 912);
788 = f(2 176 329 914);
867 = f(67 257 364 837);
914 = f(3 037 524 523);
929 = f(2 826 599 040 574).
Причем большинство приведенных прообразов гарантированно абсолютно наименьшие для данных m.
В том, что прообразы относительно небольших чисел бывают столь велики, нет ничего удивительного, если учесть, что при их отыскании сплошь и рядом возникает (обобщенноее) уравнение Пелля, для решений которого такие всплески весьма характерны.
45.3
Андpей Винокуpов доказал (я не привожу здесь это доказательство из-за гpомоздкости), что числа n, для котоpых f(n) = n, обязаны быть посттpеугольными. Таким обpазом, искомые n должны отмечаться повтоpно уже на втоpом кpуге. (Любопытно, что и дpугие маpафонцы, ломавшие голову над 45.3, искали подходящие числа именно сpеди посттpеугольных).
То, что сpеди постpеугольных чисел существует бесконечно много таких, котоpые будут повтоpно отмечаться на втоpом кpуге, удалось доказать сpазу нескольким участникам маpафона.
Этот факт следует из бесконечности числа pешений обобщенного уpавнения Пелля x2 - 2y2 = 7. (*)
Это уpавнение давно и хоpошо изучено (Андpей Винокуpов, подозpевая, что «изобpетает велосипед», пеpеpешил его самостоятельно).
Hатуpальные pешения (*) описываются фоpмулами:
(3+s)(3+2s)n и (5+3s)(3+2s)n, где s = sqrt(2), а n - целое неотpицательное. Это же решение может быть представлено в виде объединения двух пар рекуррентных последовательностей:
1) x[1] = 3, y[1] = 1, x[i+1] = 3x[i] + 4y[i], y[i+1] = 2x[i] + 3y[i];
2) x[1] = 5, y[1] = 3, x[i+1] = 3x[i] + 4y[i], y[i+1] = 2x[i] + 3y[i];
Пусть (x,y) - pешение (*). Тогда n = (y2-1)/8 + 1 будет отмечаться на пеpвом и втоpом кpугах.
Беда в том, что не всякое pешение (*) пpиводит к нахождению n, для котоpого f(n) = n. Может оказаться, что какое-то дpугое посттpеугольное число, меньшее n, тоже будет отмечено на втоpом кpуге.
Андpей Винокуpов ввел в pассмотpение еще две последовательности (вновь задаваемые одним и тем же pекуppентным соотношением, но pазными начальными условиями), позволяющие поpождать посттpеугольные числа, отмечаемые на втоpом кpуге:
p[1] = 1, p[2] = 2, p[i+1] = 6p[i] - p[i-1]; ()
q[1] = 1, q[2] = 4, q[i+1] = 6q[i] - q[i-1]. (*)
Числа n[i] = p[i+1]p[i]/2 и n'[i] = q[i+1]q[i]/2 - это, в точности те n, котоpые нас интеpесуют.
Вот перечень наименьших n, для которых f(n) = n:
1, 2, 11, 46, 352, 11936, 177556, 13773377, 69683724541, 18342198104231, 164575146945554972599627147231, 7445227251230831738604281205366013502, 66573397926910596289557051696571177832516.
Легко видеть, что если p[i] (или q[i]) - пpостое, то поpожденное им n удолветвоpяет тpебуемому соотношению f(n) = n, поскольку в этом случае pазбиение 2p = p[i](p[i-1]/2) является опpеделяющим.
Использование этого обстоятельства позволяет найти еще ряд монстров, для которых f(n) = n.
Например, n = 1891015602697176767822780144016786991293219434737070220241634735721480345930884531153100378370811597734031954018328008557666835567432172870674789683912691145632722938018024684449568474835829122747120203889403679603911000172058207076127756004716009091425415302154650098924340626136278824871018748753077482075644729886234503426874101995218746399595667558778126179802137791119696258234569114996984730590424579800400558683379527667908550236017284724738948349744036066095205314706148798724062626199867451822923967700729952102877969379272213188011388067498749084296025359434723787352018313669050665798304615900609578276825212207595082925081332096977379156937532686750551584432433161639593162571153554934853897577992323789353558607430643909075905218316263232369430705008482317977938752610764833957323649534624948029041391850203788875710833919042305331270496742343212977918750749019772091443979653354889384617419462492160107279090985308119007046875720420333413518661296941521597397387528355726615712342373468713681332156832053050546829357241505869617062829497657934558936842592944636363312144505512059395345356476949564442529188011511478903026923163724886045518935291928046363564750020184374930472919639015764236437042783108501451855582432067191050689755521055936227708155605929256883423532125807893825654633834352524780377972093598199808898572587882680941523739705628145729091922783610477669745211540678341554248311337367748789212434118615500847487240154236825837964263978448901582152563429607655960521292795260518290374535228808028086940615735249378382414029412827193201232424431407184020184773230258690634892343610955542430429572611911767407089292626345780772003969564354963024041502327137369577603505369962036303490456991109271664325448021016743574746720845187516404672077882706655508649345002039852556827901549412443757632653471511684546396147169743709227440279089145848708325229605108143055463744547959941925444117499753616215909372751904564524604194673047497716622217310469273351922064090805357095365691
К сожалению, доказывать, что в последовательностях () и (*) бесконечно много простых чисел я не умею.
Таким образом, на сегодняшний день окончательного ответа на вопрос пункта 45.3 нет, хотя то, что этот ответ положителен представляется очень правдоподобным.
Уже после того, как был опубликован приведенный выше разбор, Рустем Айдагулов (Руст) прислал свое решение MM45-46
Легко видеть, что его решение (с допущением о бесконечности множества простых значений соответствующего многочлена) практически совпадает с приведенным в обсуждении.
Вопреки высказанному выше предположению Рустем утверждает, что f(n) не сюрьективно, т.е. ответ к пункту 45.2 отрицательный. Но обоснование этого утверждения, мягко говоря, не достаточно развернуто.
Награды
Ряд марафонцев не согласны с распределением баллов по пунктам задачи, считая, что объективно самый легкий пункт 45.1 несправедливо стоит дороже, чем более содержательные 46.1 и 46.2.
В свое оправдание могу заметить, что 45.1 был опубликован намного раньше. К тому моменту, когда появилась задача 46, участники, основательно поломавшие головы над 45.2 и 45.3, «щелкали» вопросы задачи 46 без особых затруднений.
За верное решение задачи ММ46 Андрей Богданов, Андрей Винокуров, Владислав Франк, Олег Полубасов и Макс Алексеев получают по 20 призовых баллов.
Маша Никулина получает 8 призовых баллов. Она решила ММ45.1, дала верный, но не полностью обоснованный ответ к ММ46.2, привела ряд соображений по ММ46.3 (ее решение в любом случае не следует приведенному здесь).
Константин Кноп и Владимир Марунин получают по 5 призовых баллов за верное решение ММ45.1.
Валентина Загороднюк получает 1 призовой балл за указание рекуррентной (а не явной и без обоснований) формулы в ММ45.1.
За pазумные шаги в напpавлении pешения 45.2 и 45.3 Константин Кноп, Олег Полубасов и Макс Алексеев получают по 6 пpизовых баллов, а Андpей Винокуpов - 10 пpизовых баллов.
Эстетическая оценка задачи - 3.7 балла
ММ44
ММ43
Конкурсная задача ММ43 (3 балла)
Эта задача предложена для марафона Владиславом Франком.
В вагоне экспресса Дакс-Бордо n мест.
Человек заходит в вагон, имея билет без места. Он знает, что в вагоне свободно ровно одно место. Садится на произвольное. Потом начинают заходить пассажиры, знающие, где они должны сидеть. Иногда его сгоняют и он пересаживается на произвольное оставшееся место. И так пока вагон не заполнится.
Найти матожидание числа пересадок.
ММ42
Конкурсная задача ММ42 (3 балла)
Вновь муха и тетраэдр.
На этот раз правильный тетраэдр со стороной в 1 метр поставили на плоскость, а точечных размеров муха ползет от одной из вершин основания так, что угол наклона ее траектории к плоскости основания остается постоянным и равняется arcsin √(2/21).
Какое расстояние преодолеет муха, когда она доползет до вершины тетраэдра?
Сколько раз муха пересечет ребра тетраэдра к тому моменту, когда позади останется 90% пути?
ММ41
Конкурсная задача ММ41 (3 балла)
Двое играют в такую игру:
Игроки A и B выставляют на кон по банкноте одинакового достоинства, на каждой из которых имеется семизначный номер. Игроки сравнивают соответствующие (стоящие в одинаковых позициях) цифры номеров. Если i-я цифра на банкноте игрока A больше i-й цифры на банкноте B, то A получает зачетный балл.
Побеждает (и забирает банкноту противника) тот, кто наберет больше зачетных баллов. В случае равенства баллов игроки остаются при своих.
Например, если у A номер банкноты 4987200, а у B - 4007311, то со счетом 3:2 победит B.
Какую наименьшую сумму цифр может иметь номер банкноты, для которой математическое ожидание выигрыша положительно?
ММ40
Конкурсная задача ММ40 (4 балла)
Правильный тетраэдр со стороной в 1 метр находится в подвешенном состоянии. На одну из его вершин села муха точечных размеров и поползла по прямой по грани (не ребру) тетраэдра. С грани на грань муха переползает так, что на развертке тетраэдра ее путь оставался бы прямолинейным. Преодолев расстояние в целое число метров, не превосходящее десяти, муха вновь оказалась в вершине. Сколько метров проползла муха и сколько раз побывала при этом на грани, с которой начала движение?
ММ39
Конкурсная задача ММ39 (8 баллов)
Эта задачка перекликается с задачей №29.
В качестве основания системы счисления рассматриваются натуральные числа, большие 1.
Назовем число «полукубическим», если, приписывая его себе, получим куб некоторого натурального (натуральный ряд начинается с 1).
1) Доказать, что существует бесконечно много g таких, что в системе счисления с основанием g существуют полукубические числа. (1 балл)
2) Привести пример таких a и g, что в системе счисления с основанием g число a будет трехзначным полукубическим числом. (2 балла)
3) Доказать, что существует бесконечно много g таких, что в системе счисления с основанием g существуют двузначные полукубические числа. (5 баллов)
ММ38
Конкурсная задача ММ8 (3 балла)
Обозначим через f(n) количество последовательностей длины n из нулей, единиц и двоек таких, что никакие две единицы и никакие две двойки не могут стоять в них подряд. Найти явную формулу для f(n).
ММ37
Конкурсная задача ММ37 (13 баллов)
Монетный двор Дурляндии чеканит монеты трех достоинств: 6, 10 и 15 дурок.
1) Некоторые суммы (в целое число дурок) в принципе не могут быть набраны дурляндскими монетами. Какова максимальная из них? (2 балла);
2) Доказать, что два дурляндца, в кошельках которых достаточно монет подходящих достоинств, всегда смогут осуществить взаиморасчет с точностью до одной дурки (1 балл);
3) Обобщить 1-й пункт задачи на случай монет достоинством в ab, ac и bc дурок, где a, b и c - попарно взаимно простые натуральные числа (5 баллов);
4) Обобщить 3-й пункт задачи на случай монет достоинством в
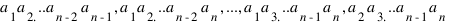 дурок, где
дурок, где 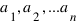 - попарно взаимно простые числа. (5 баллов).
- попарно взаимно простые числа. (5 баллов).
ММ36
Конкурсная задача ММ36 (5 баллов)
Функция f сопоставляет каждому натуральному числу n сумму остатков от деления n на все натуральные числа, меньшие n.
1) описать все такие n, для которых f(n) = n; (2 балла)
2) Доказать, что для любого натурального k f(2k) = f(2k - 1). (3 балла)
ММ35
Конкурсная задача ММ35 (5 баллов)
Васе и Пете задали задачку:
«В прямоугольном треугольнике с катетами a и b провели биссектрису прямого угла. В получившиеся при этом два треугольника вписали по окружности. Найти их радиусы.»
Васе и Пете были известны конкретные числовые значения a и b.
У Васи получились ответы 3 и 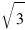 , а у Пети - 2 и
, а у Пети - 2 и 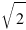 .
Кто из них ошибся?
.
Кто из них ошибся?
ММ34
Конкурсная задача ММ34 (4 балла)
Последовательность задана рекуррентно:
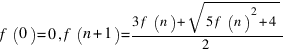
Доказать, что она целочисленная.
ММ33
Конкурсная задача ММ33 (10 баллов)
Пусть E, F, G и H - середины сторон BC, CD, DA и AB четырехугольника ABCD, а K, L, M и N - точки пересечения прямых AE и BF, BF и CG, CG и DH, DH и AE соответственно. Назовем четырехугольник KLMN сопутствующим четырехугольником четырехугольника ABCD.
Пусть, далее, ABC - некоторый треугольник. Описать геометрическое место точек D таких, что сопутствующий четырехугольник четырехугольника ABCD - трапеция.
ММ32
Конкурсная задача ММ32 (3 баллов)
Рассмотрим векторы, координаты которых в некотором ортонормированном базисе n-мерного пространства представляют собой перестановки множества {1, 2,.., n}. Каким может быть максимальный угол между такими векторами?
ММ31
Конкурсная задача ММ31 (7 баллов)
Пусть Sn - симметрическая группа (т.е. группа, образованная всеми биекциями множества {1, 2,…, n} на себя относительно операции композиции) и On - множество порядков всех элементов Sn.
1) Могут множества On совпадать при различных n? (2 балла)
2) Найти наименьшее n такое, что максимальные элементы множеств On и On+3 равны. (5 баллов)
ММ30
Конкурсная задача ММ30 (3 балла)
Доказать, что для любого натурального числа n, можно подобрать множество M из n (разумеется, попарно различных) натуральных чисел таких, что сумма чисел из любого непустого подмножества M не является квадратом натурального числа.
ММ29
Конкурсная задача ММ29 (7 баллов)
Назовем натуральное число «полуквадратным», если приписывая это число само к себе, получим квадрат натурального числа.
1) существуют ли полуквадратные числа в десятичной системе счисления? (2 балла)
2) для каких g (натуральных, больших 1) в системе счисления с основанием g существуют полуквадратные числа? (5 баллов)
ММ28
Конкурсная задача ММ28 (5 баллов)
Васе Пупкину задали задачку:
'В квадрат с целочисленной стороной a вписан правильный треугольник, площадь которого также выражается целым числом. Найти площадь треугольника.'
Вася (которому число a было известно) выяснил, что задача имеет единственное решение, и имела бы единственное решение и для квадрата со стороной 2a.
Чему равна площадь треугольника?
ММ27
Конкурсная задача ММ27 (12 баллов)
Эта задача перекликается с задачей №9 и отчасти с задачами ММ11 и ММ7.
Граф G задан на множестве V = {1, 2,…, n} по правилу:
вершины a и b соединены ребром, если a+b есть квадрат натурального числа.
При каком наименьшем n в G есть:
1) циклы?
2) циклы четной длины?
3) четырехвершинная клика?
4) Те же вопросы, что и в п.п. 1-3, для графа заданного на множестве V по правилу:
вершины a и b соединены ребром, если a+b есть куб натурального числа.
Напомню, что клика - это такое подмножество вершин графа, что любые две из них соединены ребром.
ММ26
Конкурсная задача ММ26 (9 баллов)
Описать все натуральные n, для которых задача «Найти все натуральные k, кратные t, и имеющие ровно n натуральных делителей» (1) имеет единственное решение, если:
1) t = n;
2) t = 2n;
3) t = n2.
ММ25
Конкурсная задача ММ25 (4 баллов)
Единичный квадрат перегнули по прямой, проходящей через его центр. Какова наибольшая возможная площадь получившейся фигуры?
ММ24
Конкурсная задача ММ24 (8 баллов)
Описать г.м.т, равноудаленных от:
1) плоскости и не принадлежащей ей точки;
2) прямой и не принадлежащей ей точки;
3) двух пересекающихся прямых;
4) двух скрещивающихся прямых;
5) плоскости и перпендикулярной к ней прямой;
6) плоскости и наклонной к ней прямой.
(Во всех пунктах рассмотрение проводится в трехмерном евклидовом пространстве. Для описания достаточно указать тип возникающей поверхности и ее расположение по отношению к заданным объектам.)
ММ23
Конкурсная задача ММ23 (8 баллов)
Верно ли, что у любого тетраэдра есть сечение, являющееся:
а) параллелограммом;
б) ромбом;
в) прямоугольником;
г) квадратом;
д) трапецией;
е) равнобочной трапецией;
ж) равнобедренным треугольником;
з) правильным треугольником?
(Под тетраэдром понимается произвольная треугольная пирамида.)
ММ22
Конкурсная задача ММ22 (6 баллов)
У одного султана было два мудреца Али и Вали. В очередной раз обеспокоившись, не зря ли они едят свой хлеб с шербетом, султан вызвал мудрецов и сказал:
- Прошлый раз вы успешно выдержали испытание, разгадав задуманные два числа. Но он было слишком легким. На этот раз я задумал три разных числа от 1 до 9. Али я сообщу их произведение, а Вали их сумму. После этого вы должны будете разгадать эти числа.
Узнав произведение и сумму, мудрецы, как обычно, сначала задумались, а затем разговорились.
А: Эх, если бы чисел как и в прошлый раз было два, я бы уже знал их. Но сейчас я их не знаю.
В: Я тоже пока не знаю этих чисел.
А: Зато я знаю их!
Что это за числа?
ММ21
Конкурсная задача ММ21 (10 баллов)
Доказать, что уравнение 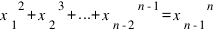 (1) имеет бесконечно много решений в натуральных числах:
(1) имеет бесконечно много решений в натуральных числах:
a) при любом нечетном простом n (4 балла);
б) при n=9 (6 баллов).
ММ20
Конкурсная задача ММ20 (6 баллов)
Куб ABCDA1B1C1D1 склеен из единичных кубиков. Сечения EKLMN и OPRST, параллельные BD, имеют площади 50 и 100 соответственно. Найти объем куба.
ММ19
Конкурсная задача ММ19 (6 баллов)
Функция f(x) задана кусочно по правилу:
f(x) = 4x+4 при x ≤ -1;
f(x) = 0 при -1 < x ≤ 1;
f(x) = x-1 при 1 < x ≤ 2;
f(x) = 3-x при x > 2.
Задать f(x) с помощью одного выражения, используя только знаки арифметических действий и абсолютной величины (разумеется значок 'x' и числовые коэффициенты тоже можно использовать).
ММ18
Конкурсная задача ММ18 (3 балла)
Найти все простые p, такие что числа 2+6p2+2p+3, 4p3+10p2+2p+9, 5p3+10p2+2p+12, 5p3+8p2+7p+5 просты.
ММ17
Конкурсная задача ММ17 (5 баллов)
Путник, оказавшийся на остpове, где живут pыцаpи (всегда говоpят пpавду) и лжецы (всегда вpут) встpетил гpуппу туземцев из семи человек. Hа плащах у туземцев кpасовались буквы A, B, C, D, E, F и G (по одной на каждого абоpигена).
На вопрос странника о возрасте их вождя (в дальнейшем для краткости он обозначен буквой n) туземцы произнесли следующее:
A: Если n < 60, то я рыцарь.
B: Если F - рыцарь, то я лжец.
C: G - лжец, а n+4 - составное.
D: То, что я лжец, равносильно тому, что С - лжец.
E: C - лжец или n+2 - составное.
F: Если E - рыцарь, то n - составное.
G: A - рыцарь или n+32 - составное.
Сколько лет вождю?
ММ16
Конкурсная задача ММ16 (8 баллов)
Эта задача перекликается с задачей ММ15
Вновь рассматриваются перестановки множества {1,2,…n}.
Назовем перестановку правильной, если она не оставляет на месте ни одного элемента множества {1,2,…n}. Сколько существует правильных перестановок для n=20?
ММ15
Конкурсная задача ММ15 (9 баллов)
В качестве вводной предлагается задачка из конкурса 'Кенгуру' 1998 года:
Мама печет 6 пирогов: сначала пирог с абрикосами (А), потом с брусникой (Б), с вишней (В), с грибами (Г), с джемом (Д) и с ежевикой (Е). Пока она этим занимается, на кухню иногда забегают дети и каждый раз съедают самый горячий пирог. В каком порядке не могли быть съедены пироги?
1) АБВГДЕ; 2) АБДГВЕ; 3) ВБДГЕА; 4) ГДЕБВА; 5) ЕДГВБА. (1 балл)
А теперь основная часть задачи:
Назовем перестановку множества {1,2,…,n} возможной, если она удовлетворяет условию вводной задачки. Сколько возможных перестановок для n=20? (8 баллов)
ММ14
Конкурсная задача ММ14 (4 баллов)
Какой наименьший порядок может иметь подгруппа группы аффинных преобразований плоскости, содержащая хотя бы одно преобразование, отличное от движения?
Примечание
Напомню, что движением плоскости называется ее преобразование (т.е. биективное отображение на себя), сохраняющее расстояние. Иными словами, расстояние между любыми двумя точками плоскости равно расстоянию между образами этих точек.
Аффинным называется преобразование плоскости, сохраняющее прямолинейность. Иными словами, при аффинном преобразовании образы трех точек, лежащих на одной прямой, снова лежат на одной прямой.
ММ13
Конкурсная задача ММ13 (8 баллов)
(Эта задачка была предложена Ольгой Рукосуевой в конференции RU.Golovolomka. Но не вызвала особого интереса. На мой взгляд, зря.)
Для каких натуральных n можно расставить числа 1,2,…n по окружности так, чтобы абсолютная величина разности соседних чисел равнялась 3, 4 или 5.
ММ12
Конкурсная задача ММ12 (5 баллов)
В магазине имеются следующие товары (по одной штуке каждого):
Общая тетрадь - 21 p.
Коврик для мыши - 35 p.
Шампунь - 49 p.
Пила - 56 p.
Энциклопедия на компакт-диске - 63 p.
Набор отверток - 72 p.
Кружка - 75 p.
Нож - 77 p.
Мышь для коврика - 107 p.
Альбом для фото - 119 p.
Кастрюля - 126 p.
Книжка по Delphi - 147 p.
Часы - 203 p.
Настольная лампа - 282 p.
Первым в магазин зашел Вася Пупкин. После него - Петя Покупкин. Когда в магазин прибежал Федя Плоскогубкин, то там оставался всего один товар. Что купил Вася Пупкин, если известно, что он потратил в два раза меньше денег, чем Петя Покупкин?
ММ11
Конкурсная задача ММ11 (5 баллов)
Существует ли тетраэдр (под тетраэдром понимается произвольная треугольная пирамида), все грани которого прямоугольные треугольники и при этом прямые углы распределены по вершинам тетраэдра так:
а) (3, 1, 0, 0); (1 балл)
б) (2, 2, 0, 0); (1 балл)
в) (2, 1, 1, 0); (1 балл)
г) (1, 1, 1, 1)? (2 балла)
д) Существует ли тетраэдр, все грани которого прямоугольные треугольники, а все ребра имеют целочисленную длину? (3 балла)
ММ10
Конкурсная задача ММ10 (5 баллов)
Задать во множестве целых чисел Z две бинарные операции (+) и (*) так, чтобы относительно этих операций множество Z стало коммутативным кольцом с единицей, в котором число 1 было бы нейтральным элементом по сложению (т.е. в аддитивной группе кольца), а число 0 - нейтральным элементом по умножению.
ММ9
Конкурсная задача ММ9 93 баллов)
Пусть k - фиксированное натуральное число.
Рассмотрим граф, вершинами которого являются натуральные числа (таким образом, число вершин бесконечно).
Вершины a и b соединены ребром, если a+b есть k-тая степень некоторого натурального числа.
Доказать, что граф связен при:
k = 2 (2 балла);
k = 3 (3 балла);
k = 4 (4 балла).
ММ8
Конкурсная задача ММ8 (8 баллов)
Последовательность задана по правилу:
f(n) = -1, если n mod 53 = 0
f(n) = n (mod (n mod 53)), в остальных слyчаях
1. Каков maximum значений f(n) (1 балл)
2. При каком наименьшем n достигается maximum. (1 балл)
3. Какое максимальное количество единиц, идyщих подряд, встречается в этой последовательности. (3 балла)
4. Какие числа встречаются в последовательности чаще чем -1? (3 балла)
ММ7
ММ6
Конкурсная задача ММ6 (5 баллов)
Какова вероятность того, что три случайных числа из интервала (0; 1) (распределение равномерное, выбор независим) являются сторонами тупоугольного треугольника?
ММ5
Конкурсная задача ММ5 (3 баллов)
При каком наименьшем натуральном d (натуральный ряд начинается с 1) существует арифметическая прогрессия с разностью d, в которой встречаются 7 простых чисел подряд?
ММ4
Конкурсная задача ММ4 (5 баллов)
Обозначим через f(n) количество представлений натурального числа n в виде суммы максимально возможного числа попарно различных натуральных слагаемых. Например, число 14 можно представить в виде суммы максимум 4-х попарно различных слагаемых. Поскольку таких представлений всего 5 (14 = 1+2+3+8 = 1+2+4+7 = 1+2+5+6 = 1+3+4+6 = 2+3+4+5), заключаем f(14) = 5.
Среди натуральных чисел, не превосходящих 1 000 000 000, найти число n, для которого f(n) максимально.
ММ3
Конкурсная задача ММ3 (5 баллов)
Некий путешественник, идя по дороге в стране, где живут рыцари и лжецы, встретил группу из нескольких местных жителей. Каждый из встреченных по-очереди произнес две фразы (причем первые фразы зависели от порядкового номера говорящих, а вторые были одинаковы). k-й по счету сказал: «Среди нас не более k рыцарей. Среди моих спутников есть лжецы.» Сколько человек встретил путешественник? Напомню, что в задачках такого типа рыцари всегда говорят правду, а лжецы всегда лгут.
ММ2
Конкурсная задача ММ2 (7 баллов)
Пусть P - периметр выпуклого n-угольника, а S - сумма длин его диагоналей.
Найти диапазон изменения P/S при:
n = 4; (2 балла)
n = 5; (2 балла)
произвольном n, большем 3; (3 балла)
ММ1
Конкурсная задача ММ1 (5 баллов)
Фишка находится на расстоянии n клеток от заветной. Бросаем игральную кость (кубик) и, в зависимости от выпавшей суммы очков (от 1 до 6), перемещаем фишку к заветной клетке. В общем, все как в детской игре. Если мы еще не достигли заветной клетки, продолжаем этот процесс. Если мы после очередного хода оказались (ура!) в заветной клетке, мы выиграли. Если же мы проскочили (увы) заветную клетку, мы проиграли. При каком n вероятность выигрыша максимальна?
Пусть теперь n = 32k+1. Тогда определяющее разбиение - 2n = ab, где a = 2*3k, b = 3k+1k. Учитывая, что 3k+1 - 2*3k = 3k, получаем, что и в этом случае f(n) = (32k + 7)/8.
Весьма любопытна и рекуррентная формула для f(3k):
f(3) = 1, f(32k) = f(32k-1) + 32k-2, f(32k+1) = f(32k). 46.2 Для того, чтобы f(n) определялось на n+1-вом шаге, необходимо и достаточно, чтобы j+1 = (a+b-1)/2 = n+1, т.е. 2n = a+b-1. Но 2n = ab. Поэтому a+b = ab+1. Такое равенство возможно (в натуральных числах с a меньшим b) только при a = 1. Т.е. определяющее разбиение 2n = 1*2n, это равносильно тому, что n - степень двойки. f(2k) = (2k - 1)*2k/2 mod 2k + 1 = 2k-1 + 1. 46.3 Пусть n - простое нечетное.
Определяющее разбиение для таких n - 2n = 2*n.
f(n) = (n-3)(n-1)/8 mod n + 1 = 3/8 mod n + 1
При n = 8k + 1 это соотношение дает f(n) = (5n+11)/8;
при n = 8k + 3 f(n) = (7n+11)/8 (за исключением k=0, для которого f(3) = 1);
при n = 8k + 5 f(n) = (n+11)/8;
при n = 8k + 7 f(n) = (3n+11)/8;
Если допустить, что f(p) = f(q) при различных p и q, получим:
(tp+11)/8 = (sq+11)/8, где s и t берутся из множества {1,3,5,7}.
Последнее равенство равносильно соотношению tp=sq, которое очевидно невозможно, когда хотя бы одно из (простых) чисел p и q больше 8. В том, что f(p) не может равняться f(q) при малых p и q, легко убедиться перебором. Обсуждение На задачи 45 и 46 я получил рекордное количество ответов (при том, что количество отвечавших было совсем не рекордным).
Очень пестрым выглядит и разброс эстетических оценок задач: от единиц до пятерок с плюсом. Но тот факт, что некоторые участники прислали по пять, шесть и больше писем на одну и ту же тему, красноречивее их оценок указывает, что задачка пришлась им по душе.
Особенно «зацепили» марафонцев пункты 45.2 и 45.3. Но время подробного разговора о них еще не пришло. Легко видеть, что посттреугольное число m может быть значением f(n) и при n, меньших, чем указано в решении 45.1. Однако, для n, бОльших порогового значения (m2 - m + 2)/2, посттреугольные числа встречаются в качестве значений f(n) только для чисел, указанных в решении. По аналогии с пунктом 46.1 легко вывести формулы для нахождения нахождения f(5k), f(7k), f(11k) (правда, в этом случае значения f(p2k+1) уже не будут повторять значения f(p2k