| Карта сайта | |
| Недавние изменения | |
| Поиск | |
| Вы посетили | |
| История страницы | |
| Вход |
Содержание
Терминология к задачам ММ197,198
Последние задачи 20-го тура посвящены триангуляции многоугольников
В задачах ММ197 и ММ198 так же, как в задачах ММ145,146,147,150, под многоугольником понимается фигура, ограниченная плоской несамопересекающейся замкнутой ломаной, никакие три последовательные вершины которой не лежат на одной прямой.
ММ200
Конкурсная задача ММ200 (8 баллов)
Обозначим через T(m) максимально возможное количество треугольников, на которые можно разрезать треугольник m прямыми. (Никаких других фигур, при разрезании возникать не должно.) При каком наименьшем m значение отношения T(m)/m достигает 4?
Примечание: 8 баллов - это условная цена задачи. Такие баллы будут начисляться за результат (и его обоснование) не хуже, чем у ведущего.
ММ199
В задаче ММ199 рассматриваются многоугольники, которые могут иметь многоугольные «дыры». Будем говорить, что данный многоугольник имеет род m, если у него m многоугольных дыр. (В частности, в ММ197 и ММ198 рассматриваются многоугольники рода 0.)
Конкурсная задача ММ199 (5 баллов)
Сколькими внутренними диагоналями и на сколько треугольников триангулируется n-угольник рода m?
ММ198
Конкурсная задача ММ198 (8 баллов)
Будем говорить, что n-угольник относится к классу s, если его можно триангулировать на n-2 треугольника внутренними диагоналями в точности s различными способами. Найти три наименьших и три наибольших значения s для n = 20.
ММ197
Конкурсная задача ММ197 (5 баллов)
Будем говорить, что n-угольник относится к классу k, если его можно разрезать на k треугольников одной прямой и нельзя разрезать одной прямой на большее число треугольников. Найти все возможные значения k для n = 2014.
Примечания:
1. Никаких других фигур при разрезании возникать не должно.
2. Если вышеописанный разрез осуществить нельзя, многоугольник относится к классу 0.
ММ196
Задача ММ 196 составлена Олегом Полубасовым по мотивам ММ186
Конкурсная задача ММ196 (9 баллов)
1. Три корабля A, B, и C движутся равномерно и прямолинейно.
2. Когда корабль A находился ближе всего к маяку, расстояние между B и C было 30 миль.
3. Когда корабль B находился ближе всего к маяку, расстояние между A и C было 40 миль.
4. Когда корабль C находился ближе всего к маяку, расстояние между A и B было 14 миль.
5. В 12:00 расстояния от маяка до всех кораблей были одинаковыми.
6. В 13:00 расстояния от маяка до всех кораблей были одинаковыми.
7. В 14:00 расстояния от маяка до всех кораблей были одинаковыми.
8. В 15:00 корабль B пересек маршрут корабля A.
9. В 16:00 корабль A пересек маршрут корабля B.
Найти скорость каждого корабля.
Примечание: Все корабли и маяк - материальные точки.
ММ195
Конкурсная задача ММ195 (7 баллов)
Доказать, что для любого натурального числа n, найдется натуральное m, такое что существует не менее n треугольников с целочисленными сторонами и медианой m.
ММ194
Конкурсная задача ММ194 (6 баллов)
Из n натуральных чисел, идущих подряд, выбрали 6 и разбили их на две тройки. При этом оказалось, что площади треугольников, стороны которых равны числам из этих троек, равны. При каком наименьшем n возможна такая ситуация?
ММ193
ММ193 (6 баллов)
Игроки Вася, Федя и Коля сыграли несколько паркий в настольный теннис навылет. Сколько партий мог сыграть Коля, если Вася сыграл a партий, а Федя - b?
Примечания: участники первой партии определяются жребием; для определенности будем считать, что b ≤ a.
ММ192
Конкурсная задача ММ192 (5 баллов)
Рассматриваются целочисленные треугольники со сторонами, не превосходящими данного натурального числа n. Каких треугольников больше: остроугольных или тупоугольных?
ММ191
Конкурсная задача ММ191 (4 балла)
Рассматриваются тройки чисел a ≤ b ≤ c, не превосходящих данного натурального числа n. Каких троек больше, тех, которые могут быть длинами сторон некоторого треугольника, или остальных?
ММ190
Настоящая геометрия
Конкурсная задача ММ190 (12 баллов)
Найти наименьшее возможное число прямых, равноудаленных от всех вершин тетраэдра?
Примечание: под тетраэдром понимается произвольная треугольная пирамида.
ММ189
Псевдогеометрия
Конкурсная задача ММ189 (6 баллов)
Для каких натуральных m существует треугольник с целочисленными сторонами и медианой m?
Для каждого подходящего m найти наибольшую возможную сторону.
ММ188
Когда трехмерный случай сложнее четырехмерного
Конкурсная задача ММ188 (9 баллов)
1. a,b,c,d - векторы трехмерного евклидова пространства (не обязательно различные). M = {{a,b,c}, {a,b,d}, {a,c,d}, {b,c,d}}. Подмножество множества M назовем хорошим, если при подходящем выборе векторов все тройки из данного подмножества образуют базис, а остальные не образуют. Сколько хороших подмножеств у M? 2. Тот же вопрос для пяти векторов в четырехмерном пространстве. 3. Тот же вопрос для пяти векторов в трехмерном пространстве.
ММ187
Можно обойтись без эллиптических кривых
Конкурсная задача ММ187 (6 баллов)
Доказать, что существует бесконечно много пар натуральных чисел 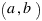 , таких что
, таких что 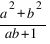 является натуральным числом.
Доказать, что существует бесконечно много пар, для которых
является натуральным числом.
Доказать, что существует бесконечно много пар, для которых 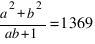 .
Существуют ли пары, для которых
.
Существуют ли пары, для которых 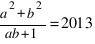 ?
?
ММ186
Еще в школе, решая задачи типа «Из пунктов A и B навстречу друг другу…», грезил предлагаемой задачей. И вот…
Конкурсная задача ММ186 (7 баллов)
В 12:00 расстояние от маяка до сухогруза «Альфа» составляло 12 км, а до буксира «Омега» - 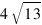 .
В 13:00 расстояния от маяка до «Альфы» и «Омеги» оказались такими же как 12:00. А в 14:00 расстояния от маяка до «Альфы» и «Омеги» оказались равны по
.
В 13:00 расстояния от маяка до «Альфы» и «Омеги» оказались такими же как 12:00. А в 14:00 расстояния от маяка до «Альфы» и «Омеги» оказались равны по 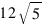 Найти минимальное расстояние от «Альфы» до «Омеги», учитывая, что в 13:45 смотритель маяка не видел «Омегу» за «Альфой».
Найти минимальное расстояние от «Альфы» до «Омеги», учитывая, что в 13:45 смотритель маяка не видел «Омегу» за «Альфой».
Примечание: Сухогруз и буксир движутся прямолинейно и равномерно. Все плавсредства и маяк - материальные точки.
ММ185
Очередной раз режем квадрат
Конкурсная задача ММ185 (5 баллов)
Квадрат со стороной 1 разрезали на 100 прямоугольников с суммой периметров P. Найти диапазон возможных значений P.
ММ184
Как же без графов?
Конкурсная задача ММ184 (7 баллов)
Компания из 30 отдыхающих собралась для 10-дневного рафтинга. Некоторые их туристов были знакомы между собой. График дежурств (по три человека на каждый день, чтобы каждый отдежурил ровно один раз) составили с помощью жребия. Получилось, что в каждой тройке дежурных ровно двое знакомы между собой. Недовольный такой ситуацией командор предложил свой график, такой что в каждой тройке была ровно одна пара незнакомых. Этот график тоже не всем понравился. Покумекав, туристы смогли совместными усилиями составить такой график, что в каждой тройке дежурных все были знакомы между собой. Какое наименьшее и наибольшее число пар знакомых могло быть в данной группе?
ММ183
Легкая задача с очевидным неочевидным обобщением
Конкурсная задача ММ183 (3 балла)
Про пять чисел a,b,c,d,e известно, что a<b<c<d<e. Попарные суммы этих чисел выписали в порядке неубывания. Найти число вариантов расположения сумм в этом списке в зависимости от конкретных значений исходных чисел.
ММ182
Продолжаем разминаться
Конкурсная задача ММ182 (3 балла)
Назовем натуральное число n суперделимым, если:
1) в каноническом разложении n имеется более двух простых делителей;
2) для любого собственного подмножества множества простых делителей число n кратно сумме элементов этого подмножества.
Доказать, что существует бесконечно много суперделимых чисел.
ММ181
Разминка
Конкурсная задача ММ181 (3 балла)
Существует ли натуральное число n, среди остатков от деления которого на все натуральные числа меньшие n чаще всего встречается остаток 2013?
MM180
Конкурсная задача ММ180 (13 баллов)
Назовем натуральное число «трижды нечетным», если само число, сумма его делителей и сумма делителей суммы его делителей нечетны. Может ли «трижды нечетное» число быть кратно 821?
MM179
Конкурсная задача ММ179(10 баллов)
Имеется 11 монет: 2 золотых; 4 серебряных; 5 бронзовых. Известно, что одна золотая, одна серебряная и 2 бронзовых монеты - фальшивые. Все настоящие монеты равны по весу. Все фальшивые тоже равны по весу, но легче настоящих. Золотые, серебряные и бронзовые отличаются друг от друга по внешнему виду. За четыре взвешивания на чашечных весах без гирь определить фальшивые монеты.
ММ178
Конкурсная задача ММ178 (Оладьи на сковородке) (9 баллов)
В единичный круг поместим (без наложений) k кругов одинакового радиуса. Обозначим через Sk максимальное значение площади этих k кругов. Расставить числа S1, S2,…, S12 в порядке возрастания.
ММ177
Конкурсная задача ММ177 (6 баллов)
В розыгрыше кубка мира участвуют 128 равных по силе шахматистов. 10 из них представляют Россию, 8 - Украину. После жеребьевки в первом раунде встречаются №1 и №2, № 3 и №4, …, №127 и №128. Во втором раунде победитель первой пары встречается с победителем второй, победитель третьей - с победителем четвертой и т. д. Российским шахматистам по жребию достались номера 1, 9, 17, 25, 33, 41, 49, 57, 65 и 73; украинским - 2, 18, 34, 50, 66, 82, 98, 114.
За первое место выплачиваются призовые - 200000 долларов, за второе - 10000 долларов.. За остальные места призовые не выплачиваются.
Какой финал более вероятен: чисто российский или чисто украинский?
Каковы российское и украинское призовые мат. ожидания?
ММ176
Конкурсная задача ММ176 (5 баллов)
Сколько точек экстремума, не являющихся точками разрыва, имеет функция f(x) = {x}+{x2}+{x}2 ?
Примечание:
{x} - дробная часть числа x.
ММ175
Конкурсная задача ММ175 (А-5) (8 баллов)
Натуральное число n назовем g-2-числом, если число 2n, записанное в системе счисления c основанием g получается из n перестановкой цифр. Какие основания встречаются (в натуральном ряду) чаще: те, для которых существуют трехзначные g-2-числа, или те, в которых нет трехзначных g-2-чисел?
Примечание: Расcматриваются позиционные системы счисления с натуральными основаниями g>1.
ММ174
Конкурсная задача ММ174 (А-4) (7 баллов)
Найти наименьшее натуральное число, произведение всех натуральных делителей которого заканчивается
а) ровно 2013 нулями;
б) не менее чем 2013 нулями.
Примечание:
Система счисления десятичная.
ММ173
Конкурсная задача ММ173 (А-3) (5 баллов)
Последовательность состоит из натуральных чисел, представимых в виде суммы четырех своих (попарно различных) делителей, расположенных в естественном порядке. Найти стомиллиардный член этой последовательности.
ММ172
Конкурсная задача ММ172 (А-2) (5 баллов)
Доказать, что существует бесконечно много хитовых abc-троек, таких что c является степенью пятерки.
Примечание:
Тройка натуральных чисел a,b,c называется хитовой abc-тройкой, если a+b = c, GCD(a,b) = 1 и c > rad(abc).
Примечание к примечанию:
Пусть 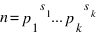 , тогда
, тогда 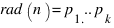
ММ171
Конкурсная задача ММ171 (А-1) (5 баллов)
Вася, Петя, Коля и Федя хвалились параллелепипедами, которые они склеили из единичных кубиков. Васин параллелепипед имел размеры axbxc. Петин - (a+1)xbxc, Колин - (a+1)x(b+1)xc, а Федин - (a+1)x(b+1)x(c+1).
- Зато у моего параллелепипеда диагональ целочисленная - сказал Вася.
- Подумаешь! У моего тоже диагональ целочисленная - заявил Петя.
- И у моего - заметил Коля.
- И у моего тоже - не отстал от товарищей Федя.
Найти максимально возможное количество честных среди перечисленных мальчиков.
ММ170
Конкурсная задача ММ170 (8 баллов)
Прямоугольный параллелепипед склеили из единичных некрашеных кубиков. После этого три грани параллелепипеда покрасили в красный цвет. Остальные три грани покрасили в синий, желтый и зеленый цвета (по одной в каждый цвет). Оказалось, что некрашеных кубиков в два раза больше, чем кубиков, имеющих, по крайней мере, одну красную грань. Количества кубиков, имеющих хотя бы одну синюю (желтую, зеленую) грань также являются делителями количества некрашеных кубиков. Найти объем параллелепипеда.
ММ169
Конкурсная задача ММ169 (6 баллов)
Для каждого натурального числа n обозначим s(n)=φ(σ(n))/σ(φ(n)), где φ(n) - функция Эйлера, а σ(n) - сумма натуральных делителей числа n. Может ли s(n) быть:
а) меньше 1/50;
б) больше 7?
ММ168
Конкурсная задача ММ168 (5 баллов)
Существует ли многогранник, у которого ровно:
2 диагонали;
5 диагоналей;
7 диагоналей?
MM167
Конкурсная задача ММ167 (4 балла)
Будем говорить, что треугольник принадлежит к классу k, если из него можно получить прикладыванием к нему другого треугольника (без наложения) ровно k различных равнобедренных треугольников. Найти все возможные значения k.
MM166
Конкурсная задача ММ166 (3 балла)
Для каждого из натуральных чисел от 1 до 10000000000 находят знакочередующуюся сумму всех натуральных делителей, упорядоченных по возрастанию (делитель 1 берется со знаком минус). Сколько отрицательных и сколько нечетных чисел при этом получится?
MM165
Конкурсная задача ММ165 (РК-5) (7 баллов)
По мотивам задачи ММ74
Вася и Петя поспорили. Вася утверждает, что объем выпуклого многогранника, все грани которого правильные многоугольники, а все 15 ребер имеют длину 1 заведомо больше объема каждого из выпуклых многогранников, о которых идет речь в задаче ММ74. Петя же утверждает, что не больше, а меньше. В качестве третейского судьи позвали Федю. Подумав, Федя пришел к выводу, что возможны разные типы выпуклых многогранников с 15-ю единичными ребрами, все грани которых - правильные многоугольники. Для одних объем, заведомо больше объема любого из многогранников из ММ74, а для других - наоборот меньше. Кто прав?
ММ164
Конкурсная задача ММ164 (РК-4) (6 баллов)
По мотивам задачи ММ135
В задаче ММ135 приведено несколько рекуррентных последовательной вида ai+1=dai-ai-1 соседние члены которых дают бесконечные множества пар натуральных чисел (a,b) таких, что остатки от деления a2 на b и b2 на a равны 2011. Существует ли натуральное число c<2000000, для которого найдется не менее 100 последовательностей с попарно различными d, соседние члены которых дают бесконечные множества пар натуральных чисел (a,b) таких, что остатки от деления a2 на b и b2 на a равны c?
ММ163
Конкурсная задача ММ163 (РК-3) (5 баллов)
По мотивам задачи ММ94 (и ММ162)
Пару похожих чисел a и b назовем s-парой, если a = spq, b=s3r, где p, q, r, s - попарно различные простые числа. Проверить истинность каждого из следующих утверждений: 1. Для каждого простого s найдется хотя бы одна s-пара. 2. Для некоторых простых s существует более одной s-пары. 3. Для каждого простого s число s-пар конечно.
MM162
Конкурсная задача ММ162 (РК-2) (4 балла)
По мотивам задачи ММ94
Пару различных натуральных чисел a и b назовем похожими, если φ(a)=φ(b), σ(a)=σ(b), τ(a)=τ(b), где φ(n), σ(n) и τ(n), соответственно функция Эйлера, сумма и число натуральных делителей числа n (см. разбор ММ94). Существуют ли похожие числа a и b такие, что τ(a)=τ(b)=4?
ММ161
Конкурсная задача ММ161 (РК-1) (3 балла)
По мотивам задачи ММ132 (и ряда других)
Граф G=<V,E> задан на множестве V = {1, 2, …, 1000000000000} по правилу: {a,b} ∈ E тогда и только тогда, когда сумма чисел a и b равна некоторой четной натуральной степени их разности. Найти число связных компонент G и диаметр наибольшей компоненты.
ММ160
Конкурсная задача ММ160 (ТГ-5) (10 баллов)
На множестве натуральных чисел от 1 до 10460353203 структура графа G задается так:
вершины a и b смежны ⇔ множества цифр в g-ичной записи чисел a и b различны при любом натуральном g ≥ 2.
Является ли G:
a) двудольным;
b) связным;
с) ациклическим?
d) Чему равна степень вершины 3?
e) Есть ли G вершины, степень которых больше чем 10000000000?
ММ159
Конкурсная задача ММ159 (6 баллов)
Для натурального числа n, большего 1, обозначим через qu(n) отношение суммы количеств единиц во всех записях числа n в системах счисления с натуральными основаниями, большими 1, к самому числу n. Найти наибольшее и наименьшее значение qu(n) и предел qu(n) при n, стремящимся к бесконечности. Конечны ли множества чисел, для которых qu(n): меньше 1; больше 1; равно 1?
Решение
ММ158
Задача ММ158 предложена Олегом Полубасовым
Конкурсная задача ММ158 (ТГ-4) (7 баллов)
I. Города занумерованы от 1 до N. Дорога, непосредственно соединяющая города i и j, существует, если и только если |i-j| - простое число. Длина дороги равна |i-j|.
Найти зависимость длины кратчайшего гамильтонова цикла от величины N.
II. Заменим в I |i-j| нат i+j.
Найти зависимость длины кратчайшего гамильтонова цикла от величины N, при условии, что полученный граф гамильтонов.
ММ157
Kонкурсная задача ММ157 (6 баллов)
В треугольнике ABC, отличном от прямоугольного, проведены высоты AE и CF, пересекающиеся в точке H. Через точки A и H проведены перпендикуляры к EF, пересекающие прямую BC в точках K и L. Найти KL, если радиус окружности, вписанной в треугольник ABC равен r, а BC = a.
ММ156
Kонкурсная задача ММ156 (ТГ-3) (5 баллов)
На занятии по дискретной математике на доске был изображен некоторый граф. Вася Пупкин записал в тетрадку количество вершин и ребер каждой связной компоненты графа, а также степени вершин самой большой (по количеству вершин) компоненты. Но само изображение графа он срисовать забыл. Кроме того, он забыл, за какую именно из вышеперечисленных характеристик отвечает каждое из записанных чисел. Сможет ли Вася решить домашнее задание «Найти диаметры каждой связной компоненты», если у него в тетрадке записаны числа: 1, 2, 2, 3, 3, 3, 4, 4, 4, 5, 6, 9?
ММ155
Конкурсная задача ММ155 (4 балла)
Существует ли цепочка из 1000 последовательных натуральных чисел, каждое из которых имеет не менее 1000 натуральных делителей?
ММ154
Конкурсная задача ММ154 (5 баллов)
Математик D предложил математикам A, B и C следующую задачку:
Я загадал два натуральных числа (не обязательно различных), каждое из которых не превосходит 20.
Сейчас я сообщу A сумму квадратов, B - произведение, а C - сумму этих чисел, а вы должны будете отгадать эти числа.
Узнав предназначенную информацию математики разговорились.
A: Я не знаю этих чисел.
B: Я тоже их не знаю.
C: И я не знаю.
B: Тогда я их знаю.
C: А я не знаю.
А: Зато я узнал их еще до того, как ты в первый раз это сказал.
Что это за числа?
MM153
Конкурсная задача ММ153 (ТГ-2) (4 балла)
Пусть n, m и k означают соответственно число вершин, ребер и связных компонент графа. Какое наименьшее количество изолированных вершин может иметь граф, для которого выполняется соотношение 11k = 10n = 8m?
ММ152
Конкурсная задача ММ152 (6 баллов)
Сколькими способами можно разрезать квадрат на 10 квадратов. Два разрезания считаются неразличимыми, если в итоге получится поровну квадратов каждого размера.
ММ151
Конкурсная задача ММ151 (ТГ-1) (4 балла)
Каждая клетка доски 4х4 покрашена либо в черный, либо в белый цвет.
На множестве клеток задана структура графа. Две клетки смежны, если: они одного цвета; у них одинаковое число соседей каждого цвета. (Соседними считаются клетки имеющие общую сторону.)
Какое наименьшее и наибольшее количество ребер может иметь такой граф, если:
а) количество клеток одного цвета может быть любым;
б) черных и белых клеток поровну?
Терминология к задачам ММ145,147,148,150
В задачах КГ12 - КГ15 будем придерживаться следующих определений и обозначений:
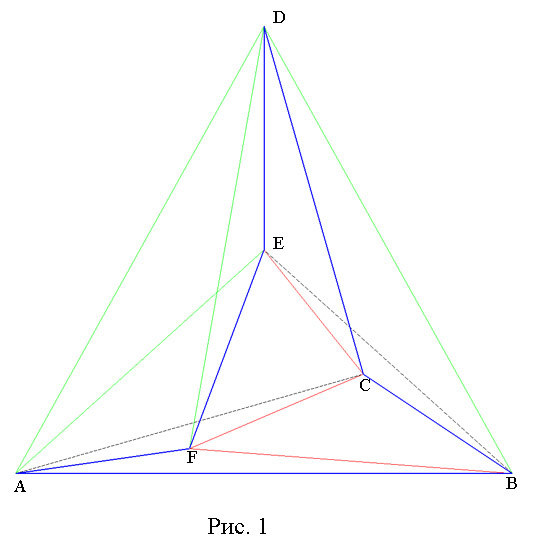
Под многоугольником мы будем понимать плоскую замкнутую несамопересекающуюся ломаную, никакие три последовательные вершины которой не коллинеарны, и часть плоскости, ограниченную этой ломаной. Число сторон исходного многоугольника обозначим через n. Назовем сторону многоугольника свободной, если продолжение этой стороны за каждую ограничивающую ее вершину в некоторой окрестности этой вершины лежит вне многоугольника. Назовем сторону полусвободной, если вне многоугольника лежит продолжение стороны ровно за одну из двух ограничивающих ее вершин. Сторону, не являющуюся ни свободной, ни полусвободной, будем называть зажатой. Например, сторона AB (рис. 1), является свободной, сторона BC - полусвободной, а сторона EF - зажатой. Диагональ, все точки которой принадлежат многоугольнику, будем называть внутренней. Диагональ, не имеющую с многоугольником общих точек, за исключением вершин, которые она соединяет, будем называть внешней. Например, диагональ BF (рис. 1) - внутренняя, а диагональ BD - внешняя (диагональ BE не является ни внешней, ни внутренней).
ММ150
Конукрсная задача ММ150 (КГ15) (12 баллов)
Каждому n-угольнику поставим в соответствие ожерелье из n бусин белого, зеленого и красного цветов следующим образом: свободой стороне соответствует белая бусина; полусвободной - зеленая; зажатой - красная. Два n-угольника назовем эквивалентными, если им соответствуют одинаковые ожерелья (ожерелье не меняется при поворотах и переворачивании). На сколько классов эквивалентности разобьются 20-угольники?
ММ149
Конкурсная задача ММ149 (8 баллов)
При каком наименьшем n в группе перестановок Sn существует подгруппа порядка 253? Привести пример такой подгруппы.
ММ148
Конкурсная задача ММ148 (8 баллов)
Сколько внутренних диагоналей может иметь n-угольник?
ММ147
Конкурсная задача ММ147 (КГ13) (6 баллов)
Какое наименьшее число внутренних диагоналей может иметь n-угольник, у которого ровно один угол больше развернутого?
ММ146
Конкурсная задача ММ146 (4 балла)
При каких D существуют графы диаметра D, у которых сумма квадратов степеней вершин равна D2?
ММ145
Конкурсная задача ММ145 (КГ12 (3 балла)
Сколько внешних диагоналей может иметь n-угольгик?
ММ144
Конкурсная задача ММ144 (5 баллов)
На поле e4 стоит чёрный король. Первый игрок ставит на любую клетку доски, не находящуюся под боем чёрного короля, белых королей (по одному за ход). Второй игрок делает (правильный) ход чёрным королём. Игра заканчивается, когда у чёрного короля не будет ходов. Каково минимальное количество ходов, за которое первый игрок может достичь цели?
ММ143
Конкурсная задача ММ143 (КГ11) (4 балла)
Девять из десяти ребер пятиугольной пирамиды имеют длину 1. В каком диапазоне может изменяться длина 10-го ребра?
ММ142
Конкурсная задача ММ142 (4 балла)
Все 80 натуральных делителей натурального числа n расположили в порядке возрастания. Оказалось, делители с первого по четвертый образуют геометрическую прогрессию, делители с четвертого по седьмой - арифметическую прогрессию, а восьмой делитель меньше 200. Найти n.
ММ141
Конкурсная задача ММ141 (3 балла)
Существуют ли натуральные числа n>1 такие, что σ(σ(n))<1.000000001n? (σ(n) - сумма натуральных делителей числа n.)
ММ140
Задача ММ140 навеяна вот этой: http://e-science.ru/forum/index.php?showtopic=26362
Конкурсная задача ММ140 (10 баллов)
На квадратной площади, разлинованной на nxn клеток (полей) собрались n2 человек, каждый из которых является либо рыцарем (всегда говорят правду), либо лжецом (всегда лгут). Каждый расположился на отдельном поле. После этого каждый произнес: «Среди моих соседей поровну рыцарей и лжецов». Какова наибольшая возможная доля рыцарей среди собравшихся?
Примечания:
n>1;
Соседними считаются поля, имеющие общую сторону;
Каждый из собравшихся знает, кем являются его соседи.
ММ139
Задача ММ139 является развитием идеи задачи Кузнецова Сергея Тихоновича. Оценка за решение этой задачи будет учитываться дважды: в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ139 (МИ5) (7 баллов)
Кнопки калькулятора расположены так, как на цифровой клавиатуре:
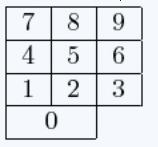
Назовём смежными те кнопки, которые имеют общую сторону или отрезок стороны (клавиша 0 смежна с клавишами 1 и 2).
Вначале на индикаторе число 0. Начинает игру Петя, прибавляя к нему любое (им выбранное) число от 0 до 9. Затем Вася прибавляет в полученному числу слагаемое, находящееся на смежной кнопке с той, которую нажимал Петя. Затем Петя делает свой ход, прибавляя число, смежное с нажатым Васей и т.д. Игра заканчивается, когда после очередного действия на индикатор появится некоторое наперёд заданное число N (N>10).
Для каких N наибольшее число вариантов первого хода Пети приведёт его в дальнейшем к победе?
Примечание: Игра заканчивается, когда после очередного действия на индикаторе появится некоторое наперёд заданное число N (N>10). Если же некоторым ходом получено число, более N, игрок, сделавший такой ход, проигрывает.
ММ138
Конкурсная задача ММ138 (6 баллов)
Доказать, что для любого натурального k найдутся натуральные a, n и g, такие что для всех i из {0,1,… ,k-1} в системе счисления с оcнованием g+i, число a является n-i-значным.
ММ137
Оценка за решение задачи ММ137 учитывается дважды: в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ137 (МИ4) (6 баллов)
Шашки двух игроков стоят на противоположный полях прямоугольника 1x(N+2), между ними N клеток. Начальная скорость каждой шашки равна 1. Каждый ходом игрок может или передвинуть свою шашку в сторону противника на величину, равную текущей скорости или увеличить скорость на 1 и передвинуть шашку в этом направлении уже на величину увеличенной скорости. Выигрывает тот, кто поставит свою шашку на шашку противника или перепрыгнет через неё. Для каких натуральных N, не превосходящих 100, выиграет второй игрок?
ММ136
Оценка за решение задачи ММ136 учитывается дважды: в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ136 (МИ3) (5 баллов)
На столе в открытую лежит 16 карт: 4 туза (считаются за 1 очко), 4 двойки, 4 тройки и 4 четвёрки. Петя и Вася по очереди берут оттуда по одной карте и складывают в отдельную стопку (общую). Выигрывает тот, после чьего хода сумма очков в этой стопке составит 21 очко (или заставивший соперника своим ходом превысить это значение). Петя начинает игру. Кто победит в игре и какой стратегии он должен придерживаться (как реагировать на ходы соперника)?
ММ135
Конкурсная задача ММ135 (4 балла)
Конечно ли множество пар натуральных чисел (a,b), таких что остатки от деления a2 на b и b2 на a равны по 2011?
ММ134
Оценка за решение задачи ММ134 учитывается дважды: в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ134 (МИ2) (4 балла)
Позицией в игре является конечное множество чисел, записанных в двоичной системе счисления. Игроки по очереди разбивают одно из чисел этого множества на части так, чтобы выполнялись два правила: 1) оба полученных числа должны начинаться с единицы; 2) хотя бы одно из них должно заканчиваться нулём. Например, 1101 можно разбить только на 110 и 1, а 11010 - на 1 и 1010 или на 110 и 10.
Проигрывает тот игрок, кто не сможет сделать ход согласно правилам.
Кто выиграет, если игра начнётся с числа (2011)10=(11111011011)2?
ММ133
Оценка за решение задачи ММ133 учитывается дважды: в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ133 (3 балла)
На столе лежит N спичек. Петя и Вася поочерёдно берут оттуда от 1 до 5 спичек, однако нельзя повторять число, взятое соперником на предыдущем ходу. Выигрывает тот, кто забирает последнюю спичку. Начинает Петя, своим первым ходом может взять любое количество от 1 до 5. Найдите общий вид чисел N, при которых партию выиграет Вася.
ММ132
Конкурсная задача ММ132 (5 баллов) (Здравствуй 2011-й)
Граф G=<V,E> задан на множестве V = {1, 2,…, 2011} по правилу: {x,y} ∈ E ⇔ |x-y| > a , где a - фиксированное натуральное число, меньшее 1006.
Сколько периферийных вершин может иметь граф G?
Примечание: Вершина графа называется периферийной, если ее эксцентриситет равен диаметру графа.
ММ131
Конкурсная задача ММ131 (3 балла) (Прощай 2010-й)
Граф G=<V,E> задан на множестве V = {1, 2, …, 2010} по правилу: {x,y} ∈ E ⇔ x+y = a или x+y = b, где a и b - фиксированные натуральные числа.
При каких a и b, граф G:
а) связен;
б) является деревом;
в) является цепью;
г) имеет циклы?
ММ130
Конкурсная задача ММ130
Комната имеет форму прямоугольного параллелепипеда шириной a, высотой b и длиной c. На стене aхb сидит таракан. Он находится на расстоянии a/2 от смежной стены и на расстоянии x от потолка, x ≤ b/2 и хочет попасть в точку, симметричную исходной относительно центра параллелепипеда.
Для некоторых значений a, b, c кратчайший путь между этими точками будет проходить через одну и ту же последовательность граней при любом x, 0 ≤ x ≤ b/2. Для каждой такой последовательности граней приведите пример тройки a, b, c.
Примечание: термин «кратчайший путь» означает путь, для которого нельзя найти путь, более короткий.
ММ129
Конкурсная задача ММ129
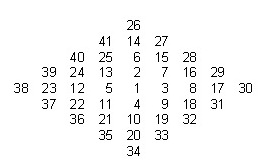
Будем заполнять бесконечный клетчатый лист бумаги натуральными числами по спирали (каждый следующий виток начинается на вертикали, в которой стоит единица):
Для каждого числа найдём восемь модулей разности его с соседями (по вертикали, горизонтали и диагонали). Количество простых чисел среди этих восьми назовем индексом простоты окружения исходного сила. Какое наибольшее значение может принимать индекс простоты окружения? Для скольких чисел достигается это значение?
Терминология ММ 121, ММ122,ММ125, ММ127, ММ128
В рамках 13-го тура, как обычно, проводился тематический конкурс. Он являлся прямым продолжением тематического конкурса из 11-го тура. Его тематика - комбинаторная геометрия.
Более того, тематические задачи тура, как и задачи ММ57, ММ101, ММ102, ММ103, ММ104 и ММ120, так или иначе связаны с выпуклыми многоугольниками. Ниже приведен ряд определений и обозначений, используемых в задачах тематического конкурса.
Число сторон исходного выпуклого многоугольника всегда обозначается через n (если иное не оговорено в конкретной задаче).
Исхоный многоугольник разбивается своими диагоналями на элементарные.
Точка внутри многоугольника называется особой (полюсом), если в ней пересекаются не менее трех диагоналей.
Если в особой точке пересекаются k диагоналей, то она является полюсом порядка k-2.
Многоугольник без особых точек будем называть ординарным, иначе - особенным.
Структурным графом выпуклого многоугольника будем называть граф, вершинами которого служат вершины и точки пересечения диагоналей исходного многоугольника, а ребрами - отрезки диагоналей и стороны исходного многоугольника.
Дуальный граф - граф геометрически двойственный структурному (вершины - грани плоской укладки структурного графа, две вершины смежны, если соответствующие грани имеют общую сторону).
Сопровождающий граф - дуальный граф без вершины, соответствующей внешней грани.
Будем называть два выпуклых многоугольника изотопными, если изоморфны их структурные графы.
В задаче ММ104 было введено понятие изоморфизма многоугольников. Изоморфными назывались многоугольники, сопровождающие графы которых изоморфны. Можно доказать, что два выпуклых многоугольника изоморфны тогда и только тогда, когда они изотопны. Мы не стали предлагать это утверждение в качестве марафонской задачи. Желающие убедиться в его справедливости могут сделать это самостоятельно (или с помощью книжек: см., например, А.А.Зыков. Основы теории графов).
Пусть n>5. Характеристическим вектором n-угольника будем называть набор s = (s1, s2, …, sm), где m = [n/2]-2, sk - число полюсов порядка k.
Два многоугольники будем называть изополярными, если равны их характеристические векторы.
Вектором граней многоугольника будем называть набор t = (t3, t4, …, tn), где tk - количество элементарных k-угольников.
Два многоугольника будем называть однотипными, если равны их векторы граней.
ММ128
Оценка за решение задачи ММ128 учитывается дважды в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ128 (КГ-10) (20 баллов)
На сколько классов изополярных восьмиугольников разбиваются выпуклые восьмиугольники?
ММ127
Оценка за решение задачи ММ127 учитывается дважды в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ127 (КГ-9) (12 баллов)
Существуют ли однотипные, но не изополярные многоугольники?
ММ126
Конкурсная задача ММ126 (4 балла)
Есть 8 шаров, среди которых 6 заряжены нейтрально, один - положительно и один - отрицательно. Есть прибор, который, будучи поднесённым к группе шаров, покажет их общий заряд (он покажет 0 и если в группе нет ни одного заряженного шара, и если они там оба). За какое наименьшее число измерений можно найти положительный и отрицательный шары в группе?
ММ125
Оценка за решение задачи ММ125 учитывается дважды в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ125 (КГ-8) (4 балла)
Верно ли, что группа автоморфизмов структурного графа любого n-угольника изоморфна подгруппе группы диэдра n-й степени?
ММ124
Конкурсная задача ММ124 (4 балла)
Пусть Sn = 2 + 3 + 5 + 7 +…+ pn - сумма n первых простых чисел. Доказать, что Sn является простым тогда и только тогда, когда существует такое простое число q, что Sn + q кратно 2, 3, 5, …, pn.
ММ123
Конкурсная задача MM123 (5 баллов)
Квадратная монета со стороной 1 см бросается случайным образом на лист бумаги, разлинованный квадратными клетками со стороной 2 см. Какая вероятность того, что монета попадёт целиком в клетку?
ММ122
Задача ММ122 является прямым продолжением задачи ММ57. Оценка за решение задачи ММ122 учитывается дважды в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ122 (КГ-7) (4 балла)
1. Найти формулу для выражения числа вершин структурного графа с данным характеристическим вектором.
2. Найти формулу для выражения числа элементарных многоугольников исходного многоугольника с данным характеристическим вектором.
ММ121
Задача ММ121 является прямым продолжением задачи ММ104. Оценка за решение задачи ММ121 учитывается дважды в основном Марафоне и в тематическом конкурсе.
Конкурсная задача ММ121 (КГ-6) (8 баллов)
1. На сколько классов однотипных семиугольников разбиваются выпуклые семиугольники? 2. На сколько классов изотопных семиугольников разбиваются выпуклые семиугольники?
ММ120
Задача ММ120 утратила статус конкурсной и может свободно обсуждаться на форуме.
Задача ММ120 продолжает линию задачи ММ57 и тематического конкурса 11-го тура.
Конкурсная задача ММ120 (7 баллов)
В задаче ММ103 каждому выпуклому многоугольнику был поставлен в соответствие сопровождающий граф: вершины графа - элементарные многоугольники, на которые разбивается исходный многоугольник своими диагоналями; две вершины смежны, если соответствующие многоугольники имеют общую сторону.
Найти возможные значения диаметра и радиуса, а также возможные количества периферийных и центральных вершин сопровождающего графа произвольного выпуклого n-угольника.
ММ119
Задача ММ119 утратила статус конкурсной и может свободно обсуждаться.
Конкурсная задача ММ119 (Ш-5) (8 баллов)
Придумать корректную (т.е. ее можно получить из начальной по всем правилам шахматной игры) позицию, в которой белые дают мат в один ход, как можно бОльшим числом способов.
Примечания:
1. Корректность позиции обосновывается указанием ходов к ней приводящих.
2. 8 баллов - это условная цена задачи. Их можеть быть и меньше, и больше, в зависимости от достигнутого результата.
Дополнительные призовые баллы могут быть начислены за обоснование неулучшаемости предложенного решения (однако их будет не больше, чем за решение, которое окажется лучше неулучшаемого) :)
ММ118
Задача о задаче (нестареющая классика на новый лад).
Конкурсная задача ММ118 (7 баллов)
Ведущий Математического марафона придумал задачу. Но, прежде чем помещать ее в Марафон, он решил протестировать задачу и рассказал ее своему коллеге:
- Бывшие одноклассники Петр и Николай встретились на мероприятии, посвященном 40-ю выпуска из школы, и разговорились.
П: Да-а… разбросала нас жизнь, 40 лет тебя не видел и ничего о тебе не слышал. А ведь раньше не разлей вода были, за одной партой сидели. Ну и как ты? Семьей обзавелся?
Н: А как же! У меня три красавца сына!
П: Ну ты даешь! И сколько же им лет?
Н: Надеюсь, ты по-прежнему любишь головоломки? Тогда догадайся сам. Сумма их возрастов равна номеру квартиры, в которой ты жил в школьные годы, а произведение возрастов равно…
… И ведущий Марафона для удобства коллеги написал нужное число на бумажке и продолжил:
- Петр достал ручку и на несколько минут погрузился в вычисления…
П: Ты знаешь, этих данных мне мало.
Н: Ах, да! Забыл добавить, что среднего я назвал в твою честь.
П: Спасибо! Теперь информации достаточно.
Сколько лет сыновьям Николая?
Коллега ведущего погрузился в вычисления (более продолжительные, чем Петр из задачи). Но его комментарий, не отличался от комментария Петра:
- Ты знаешь, этих данных мне мало - сказал он ведущему Марафона.
- Ах, да! - осознал ошибку ведущий - Тогда пусть Петром зовут не среднего, а старшего сына Николая.
- К сожалению, это не спасет задачу. А вот если Николай назовет Петром своего младшего сына, тогда задача будет иметь единственное решение!
Что за число написал ведущий?
ММ117
Задача ММ117 утратила статус конкурсной и может свободно обсуждаться.
Призовые баллы за решение ММ117 учитываются дважды: в тематическом конкурсе и в основном Марафоне. А сама задача ММ117 является прямым продолжением задачи ММ115 и так же как ММ115 предложена Сергеем Половинкиным.
Конкурсная задача ММ117 (Ш-4) (7 баллов)
На шахматной доске расставлено 64 белых коня. Какое минимальное количество коней нужно заменить черными, так чтобы в полученной позиции, действуя по правилам задачи ММ115, было бы невозможно получить хотя бы один одноцветный квадрат 5Х5? Каково количество таких позиций?
ММ116
Задача ММ116 навеяна обсуждением одной из последовательностей в OEIS.
Конкурсная задача ММ116 (10 баллов)
Сколько существует связных графов, таких что произведение степеней вершин равно:
а) сумме степеней вершин;
б) сумме квадратов степеней вершин?
ММ115
Задача ММ15 составлена специально для Математического марафона Сергеем Половинкиным.
Призовые баллы за решение ММ115 учитываются дважды: в тематическом конкурсе и в основном Марафоне.
Конкурсная задача ММ115 (Ш-3) (10 баллов)
На шахматной доске расставлены кони.
Разрешается менять цвет фигур одновременно в клетках на одной вертикали, горизонтали или диагонали (в частности, в одной угловой клетке - считается, что она сама - диагональ). Можно ли получить одноцветный квадрат 5×5 в каком-либо месте доски?
ММ114
Конкурсная задача ММ114 (7 баллов)
Спорный участок имеет форму правильного треугольника периметром 100 м.
Х, отстаивающий свое право собственности, решил для надежности обнести участок забором и приобрел 100 м сетки-рабицы.
Но к тому моменту, когда X закупил сетку, состоялся суд, присудивший разделить спорный участок между X и Y.
Линия раздела прошла по прямой через центр участка. А Y тут же оградил свою часть. Когда X оградил свою, у него
осталось 47 метров неиспользованной сетки.
Найти площади участков, доставшихся X и Y.
ММ113
Результат Задачи ММ113 учитывается дважды: в тематическом конкурсе и в основном Марафоне.
Конкурсная задача ММ113 (Ш-3) (10 баллов)
На множестве полей шахматной доски определим структуру графа GN следующим образом:
две вершины (два поля) будем считать смежными, если конь может за один ход переместиться из одной вершины в другую.
Аналогично определим граф слона GB, граф ладьи GR, граф ферзя GQ и граф короля GK.
Для каждого из этих графов:
1. Найти
а) количество ребер;
б) количество компонент связности;
в) радиус и диаметр каждой компоненты;
г) наибольшую клику.
2. Выяснить является ли граф:
а) двудольным;
б) эйлеровым;
в) гамильтоновым;
г) планарным?
ММ112
Светлой памяти C5 ЕГЭ посвящается.
Конкурсная задача ММ112 (6 баллов)
Решить уравнение при всех возможных наборах значений параметров a и b:
11x+a2-2a+b2+4b+|2x+a2-2a+4b+b2|+|-3x+2+a2-2a-4b-b2|+|-x-4b-b2+a2-2a|+18|x-2|=20
ММ111
Результат Задачи ММ111 учитывается дважды: в тематическом конкурсе и в основном Марафоне.
Конкурсная задача ММ111 (Ш-1) (3 балла)
Найти количество способов, которыми за наименьшее возможное число ходов из начальной позиции может быть получена позиция на диаграмме.

Примечание:
Ходы должны делаться по всем правилам шахматной игры.
ММ110
Конкурсная задача ММ110 (КГ-5) (6 баллов)
Квадрат со стороной n (n - натуральное, большее 1) разрезали на 4 прямоугольника с целочисленными сторонами. Сколько различных значений может принимать сумма периметров полученных прямоугольников при всех таких разрезаниях?
ММ109
Конкурсная задача ММ109 (6 баллов)
Тремя семействами параллельных линий плоскость разрезана на равные треугольники.
Можно ли в каждый треугольник вписать одно из чисел 1, 2, 3 так, чтобы:
1) хотя бы в один треугольник была вписана тройка;
2) число в каждом треугольнике указывало, сколько различных чисел написано в
трех треугольниках, имеющих общую сторону с данным?
ММ108
Задачка с антресолей.
Конкурсная задача ММ108 (4 балла)
Однородную пирамиду разрезали на слои равной толщины плоскостями, параллельными основанию. При каком наименьшем количестве частей их можно будет разложить на разные чаши равноплечных весов без гирь так, чтобы весы уравновесились?
ММ107
Наталия Макарова предложила посвятить целый тур Марафона любимым ею магическим и латинским квадратам. К столь радикальным шагам я пока не готов, но, в порядке эксперимента, предлагаю участникам «квадратную» задачку, навеянную предлагаемыми задачами, но значительно более простую.
Конкурсная задача ММ107 (4 балла)
Существует ли магический квадрат 3х3, составленный и попарно различных простых чисел, магическая сумма которого, тоже простое число?
Примечание:
Магический квадрат - это квадратная матрица, у которой сумма элементов каждой
строки (столбца, большой диагонали) равна одному и тому же числу (магической
сумме).
ММ106
Некоторые из марафонских задач привели к появлению новых последовательностей в OEIS. Макс Алексеев предложил использовать обратный механизм.
Конкурсная задача №106 (от 3 баллов)
Последовательность A116983 из OEIS определяется так:
a(n) есть порядковый номер n! при лексико-графическом упорядочении наборов
цифр числа n! (система счисления десятичная). Последнее число, представленное
в OEIS, - a(14). Требуется найти еще несколько членов A116983.
Примечание:
Три балла будут присуждаются за нахождение a(15). За нахождение большего числа
членов последовательности можно заработать больше баллов (но шкала, конечно,
не линейная).
ММ105
Конкурсная задача ММ105 (6 баллов)
Математик C загадал некий граф и сообщил математику A степени всех вершин,
а математику B - количество вершин и число связных компонент этого графа.
Дальше, как водится, состоялся обмен мнениями.
A: Знание степеней всех вершин графа не позволяет мне однозначно определить,
какой граф был загадан.
B: Зато я теперь в состоянии сделать это.
Сколько ребер было в загаданном графе?
Примечание:
Рассматриваются классические графы (неориентированные, без петель и кратных
ребер).
ММ104
Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задач ММ57, ММ101, ММ102 и ММ103.
Конкурсная задача ММ104 (КГ-4) (9 баллов)
Два выпуклых n-угольника назовем изоморфными, если изоморфны их сопровождающие графы.
Два выпуклых n-угольника назовем однотипными, если в разбиениях этих многоугольников на элементарные присутствует поровну треугольников, поровну четырехугольников и т.д.
1. Имеется ли логическая зависимость между однотипностью и изоморфностью
выпуклых многоугольников?
2. На сколько классов однотипных семиугольников разбиваются ординарные
семиугольники?
3. На сколько классов изоморфных семиугольников разбиваются ординарные
семиугольники?
ММ103
Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задач ММ57, ММ101 и ММ102.
Конкурсная задача ММ103 (КГ-3) (3 балла)
Сопоставим каждому выпуклому многоугольнику (сопровождающий) граф по следующему
правилу:
вершинами графа будут элементарные многоугольники;
две вершины смежны, если соответствующие многоугольники имеют общую сторону.
1. Доказать, что сопровождающий граф любого выпуклого многоугольника
является планарным и двудольным.
2. Сформулировать условие ординарности многоугольника в терминах
сопровождающего графа.
ММ102
Баллы, полученные за решение данной задачи учитываются дважды:
в основном Марафоне и в тематическом конкурсе.
А сама задача является прямым продолжением задач ММ57 и ММ101.
Конкурсная задача ММ102 (КГ-2) (9 баллов)
На какое наименьшее число частей может разбиваться диагоналями выпуклый n-угольник
при:
a) n = 6;
b) n = 7;
c) n = 8;
d) n = 9?
Примечание:
Цена задачи указана весьма условно.
Я не умею строго обосновывать минимальность известных мне разбиений не для всех указанных n.
Соответственно и сами известные мне ответы могут оказаться неверными.
9 призовых баллов будет присуждаться за решения аналогичые моему (имеющие тот же
ответ и ту же степень строгости его обоснования).
За улучшение известных мне ответов, получение более строгих обоснований, получение
(хотя бы частично) обоснованных ответов для бОльших n будут начисляться дополнительные
призовые баллы.
ММ101
Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задачи ММ57.
Конкурсная задача ММ101 (КГ-1) (8 баллов)
Назовем многоугольник ординарным (термин «регулярный», использованный в задаче №57, явно неудачен), если он выпуклый и никакие 3 его диагонали не пересекаются в одной точке внутри многоугольника. Пусть n - число сторон ординарного многоугольника. Ординарный многоугольник разбивается своими диагоналями на многоугольники, которые мы будем называть элементарными. Начиная с какого n, число элементарных четырехугольников может превысить число элементарных треугольников?